
【题目】如图,直线AC与⊙O相切于点A,点B为⊙O上一点,且OC⊥OB于点O,连接AB交OC于点D.
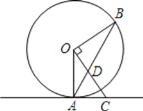
(1)求证:AC=CD;
(2)若AC=3,OB=4,求OD的长度.
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在一节数学活动课上,老师带领同学们借助几何画板对以下题目进行了研究.如图1,
MN是过点A的直线,点C为直线MN外一点,连接AC,作∠ACD=60°,使AC=DC,在MN上取一点B,使∠DBN=60°.
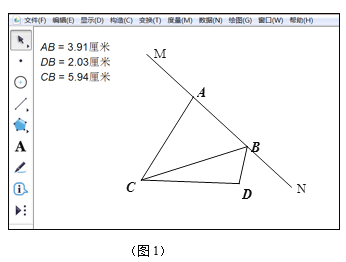
观察发现
(1)根据图1中的数据,猜想线段AB、DB、CB之间满足的数量关系是 ;
(2)希望小组认真思考后提出一种证明方法:将CB所在的直线以点C为旋转中心,逆时针旋转60°,与直线MN交于点E,即可证明(1)中的结论. 请你在图1中作出线段CE,并根据此方法写出证明过程;
实践探究
(3)奋进小组在继续探究的过程中,将点C绕点A逆时针旋转,他们发现当旋转到图2和图3的位置时,∠DBN=120°,线段AB、BD、CB的大小发生了变化,但是仍然满足一定的数量关系,请你直接写出这两种关系:
在图2中,线段AB、DB、CB之间满足的数量关系是 ;
在图3中,线段AB、DB、CB之间满足的数量关系是 ;
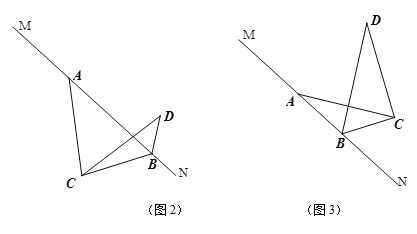
提出问题
(4)智慧小组提出一个问题:若图3中BC⊥CD于点C时,BC=2,则AC为多长?请你解答此问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,点A1,A2,A3,…都在x轴上,点C1,C2,C3,…都在直线y=![]() x+
x+![]() 上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是__.
上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是__.
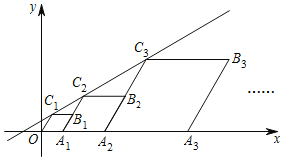
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF,②BF=![]() ,③AF=
,③AF=![]() ,④S△MEF=
,④S△MEF=![]() 中正确的是
中正确的是![]()
![]()
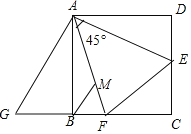
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
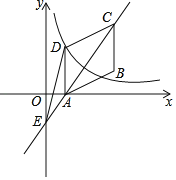
(1)写出D点坐标;
(2)求双曲线的解析式;
(3)作直线AC交y轴于点E,连结DE,求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c>0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )
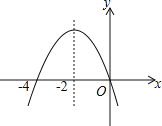
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有一栋教学楼AB,小明(身高忽略不计)在教学楼一侧的斜坡底端C处测得教学楼顶端A的仰角为68°,他沿着斜坡向上行走到达斜坡顶端E处,又测得教学楼顶端A的仰角为45°.已知斜坡的坡角(∠ECD)为30°,坡面长度CE=6m,求楼房AB的高度.(结果精确到0.1m,参考数据:tan68°≈2.48,![]() ≈1.73)
≈1.73)
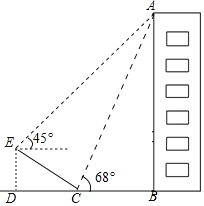
查看答案和解析>>
科目:初中数学 来源: 题型:
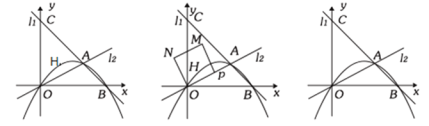
【题目】如图,在平面直角坐标系中,已知直线![]() 与直线
与直线![]() 相交于点A,与
相交于点A,与![]() 轴相交于点B,与
轴相交于点B,与![]() 轴相交于点C,抛物线
轴相交于点C,抛物线![]() 经过点O、点A和点B,已知点A到
经过点O、点A和点B,已知点A到![]() 轴的距离等于2.
轴的距离等于2.
(1)求抛物线的解析式;
(2)点H为直线![]() 上方抛物线上一动点,当点H到
上方抛物线上一动点,当点H到![]() 的距离最大时,求点H的坐标;
的距离最大时,求点H的坐标;
(3)如图,P为射线OA的一个动点,点P从点O出发,沿着OA方向以每秒![]() 个单位长度的速度移动,以OP为边在OA的上方作正方形OPMN,设正方形POMN与△OAC重叠的面积为S,设移动时间为t秒,直接写出S与t之间的函数关系式.
个单位长度的速度移动,以OP为边在OA的上方作正方形OPMN,设正方形POMN与△OAC重叠的面积为S,设移动时间为t秒,直接写出S与t之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com