
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
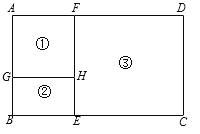
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
【答案】(1)48-12x;(2)x为1或3;(3)x为2时,区域③的面积最大,为240平方米
【解析】
(1)将DF、EC以外的线段用x表示出来,再用96减去所有线段的长再除以2可得DF的长度;
(2)将区域③图形的面积用关于x的代数式表示出来,并令其值为180,求出方程的解即可;
(3)令区域③的面积为S,得出x关于S的表达式,得到关于S的二次函数,求出二次函数在x取值范围内的最大值即可.
(1)48-12x
(2)根据题意,得5x(48-12x)=180,
解得x1=1,x2=3
答:x为1或3时,区域③的面积为180平方米
(3)设区域③的面积为S,则S=5x(48-12x)=-60x2+240x=-60(x-2)2+240
∵-60<0,∴当x=2时,S有最大值,最大值为240
答:x为2时,区域③的面积最大,为240平方米


科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践:
问题情境
数学活动课上,老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示:如图I,在正方形![]() 中,点
中,点![]() 为边
为边![]() 的中点.将
的中点.将![]() 以点
以点![]() 为旋转中心,顺时针方向旋转,当点
为旋转中心,顺时针方向旋转,当点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上时,连接
上时,连接![]() .
.

“兴趣小组”发现的结论是:![]() ;
;
“卓越小组”发现的结论是:![]() .
.
解决问题
(1)请你证明“兴趣小组”和“卓越小组”发现的结论;
拓展探究
证明完“兴趣小组”和“卓越小组”发现的结论后,“智慧小组”提出如下问题:如图2,连接![]() ,若正方形
,若正方形![]() 的边长为
的边长为![]() ,求出
,求出![]() 的长度.
的长度.
(2)请你帮助智慧小组写出线段![]() 的长度.(直接写出结论即可)
的长度.(直接写出结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
查看答案和解析>>
科目:初中数学 来源: 题型:
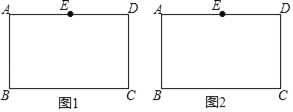
【题目】如图,在矩形ABCD中,点E为AD的中点,不用圆规、量角器等工具,只用无刻度的直尺作图.
(1)如图1,在BC上找点F,使点F是BC的中点;
(2)如图2,连接AC,在AC上取两点P,Q,使P,Q是AC的三等分点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() 、
、![]() ,交
,交![]() 轴于
轴于![]() ,直线
,直线![]() 平行于
平行于![]() 周,与抛物线另一个交点为
周,与抛物线另一个交点为![]() .
.
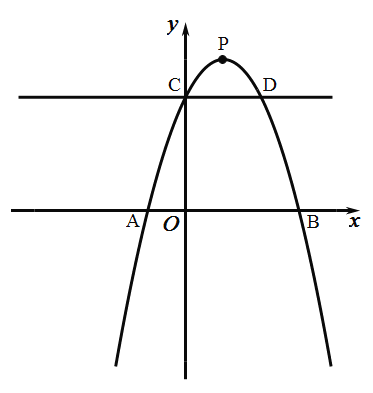
(1)求函数的解析式;
(2)若![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 是抛物线上的动点,求使以
是抛物线上的动点,求使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形的
为顶点的四边形是平行四边形的![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
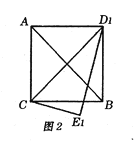
【题目】把一副三角板按如图1所示放置,其中点![]() 在
在![]() 边上,
边上,![]() ,斜边
,斜边![]() .将三角板
.将三角板![]() 绕点
绕点![]() 顺时针旋转,记旋转角为
顺时针旋转,记旋转角为![]() .
.
(1)在图1中,设![]() 与
与![]() 的交点为
的交点为![]() ,则线段AF的长为 ;
,则线段AF的长为 ;
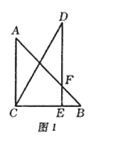
(2)当![]() 时,三角板
时,三角板![]() 旋转到
旋转到![]() ,的位置(如图2所示),连接
,的位置(如图2所示),连接![]() ,请判断四边形
,请判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
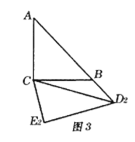
(3)当三角板![]() 旋转到
旋转到![]() 的位置(如图3所示)时,此时点
的位置(如图3所示)时,此时点![]() 恰好在
恰好在![]() 的延长线上.①求旋转角
的延长线上.①求旋转角![]() 的度数;②求线段
的度数;②求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com