
【题目】在同一平面直角坐标系中,函数![]() 与
与![]() 的图象可能是( )
的图象可能是( )
A.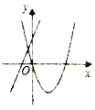 B.
B.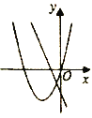 C.
C.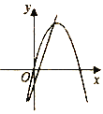 D.
D.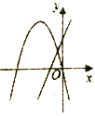
【答案】A
【解析】
先根据图形中给出的一次函数图像确定a,b的符号,进而运用二次函数的性质判断图形中给出的二次函数的图像是否符合题意,根据选项逐一讨论解析,即可解决问题.
A:对于直线y=bx+a来说,由图像可以判断,a>0,b>0;对于抛物线![]() 来说,对称轴
来说,对称轴![]() >0,应在y轴右侧,符合题意,故选A.
>0,应在y轴右侧,符合题意,故选A.
B: 对于直线y=bx+a来说,由图像可以判断,a<0,b<0;对于抛物线![]() 来说,开口应向下,不符合题意,图像错误.
来说,开口应向下,不符合题意,图像错误.
C:对于直线y=bx+a来说,由图像可以判断,a<0,b>0;对于抛物线![]() 来说,开口向下,对称轴
来说,开口向下,对称轴![]() <0,应在y轴左侧,不符合题意,图像错误.
<0,应在y轴左侧,不符合题意,图像错误.
D:对于直线y=bx+a来说,由图像可以判断,a>0,b>0,;对于抛物线![]() 来说,开口向下,a<0,不符合题意,图像错误.
来说,开口向下,a<0,不符合题意,图像错误.
故选A.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+m.
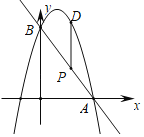
(1)如图,二次函数的图象过点A(3,0),与y轴交于点B,求直线AB和二次函数图象的解析式;
(2)在线段AB上有一动点P(不与A,B两点重合),过点P作x轴的垂线,交抛物线于点D,是否存在一点P使线段PD的长有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
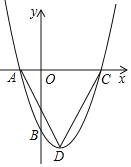
【题目】如图,抛物线y=x2+bx+c与x轴交于A,C两点,与y轴交于B点,抛物线的顶点为点D,已知点A的坐标为(﹣1,0),点B的坐标为(0,﹣3).
(1)求抛物线的解析式及顶点D的坐标.
(2)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
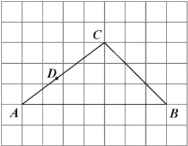
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 为
为![]() 边上的一点.
边上的一点.
(Ⅰ)线段![]() 的值为______________;
的值为______________;
(Ⅱ)在如图所示的网格中,![]() 是
是![]() 的角平分线,在
的角平分线,在![]() 上求一点
上求一点![]() ,使
,使![]() 的值最小,请用无刻度的直尺,画出
的值最小,请用无刻度的直尺,画出![]() 和点
和点![]() ,并简要说明
,并简要说明![]() 和点
和点![]() 的位置是如何找到的(不要求证明)___________.
的位置是如何找到的(不要求证明)___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com