
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 为
为![]() 边上的一点.
边上的一点.
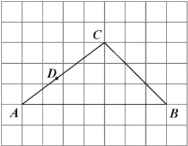
(Ⅰ)线段![]() 的值为______________;
的值为______________;
(Ⅱ)在如图所示的网格中,![]() 是
是![]() 的角平分线,在
的角平分线,在![]() 上求一点
上求一点![]() ,使
,使![]() 的值最小,请用无刻度的直尺,画出
的值最小,请用无刻度的直尺,画出![]() 和点
和点![]() ,并简要说明
,并简要说明![]() 和点
和点![]() 的位置是如何找到的(不要求证明)___________.
的位置是如何找到的(不要求证明)___________.
【答案】(Ⅰ)![]() (Ⅱ)如图,取格点
(Ⅱ)如图,取格点![]() 、
、![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() .
.
【解析】
(Ⅰ)根据勾股定理进行计算即可.
(Ⅱ)根据菱形的每一条对角线平分每一组对角,构造边长为5的菱形ABEC,连接AE交BC于M,即可得出![]() 是
是![]() 的角平分线,再取点F使AF=5,则根据等腰三角形的性质得出点C与F关于AM对称,连接DF交AM于点P,此时
的角平分线,再取点F使AF=5,则根据等腰三角形的性质得出点C与F关于AM对称,连接DF交AM于点P,此时![]() 的值最小.
的值最小.
(Ⅰ)根据勾股定理得AC=![]() ;
;
故答案为:5.
(Ⅱ)如图,如图,取格点![]() 、
、![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,则点P即为所求.
,则点P即为所求.

说明:构造边长为5的菱形ABEC,连接AE交BC于M,则AM即为所求的![]() 的角平分线,在AB上取点F,使AF=AC=5,则AM垂直平分CF,点C与F关于AM对称,连接DF交AM于点P,则点P即为所求.
的角平分线,在AB上取点F,使AF=AC=5,则AM垂直平分CF,点C与F关于AM对称,连接DF交AM于点P,则点P即为所求.


科目:初中数学 来源: 题型:
【题目】如图,在小正形的边长均为1的方格纸中,线段AB,点A,B均在小正方形的顶点上.
(1)在图①中画出平行四边形ABCD,且四边形ABCD的面积为6,点C、D均在小正方形的顶点上;
(2)在图②中画出一个△ABC,点C在小正方形的顶点上,且BC=BA,请直接写出∠BCA的余弦值.
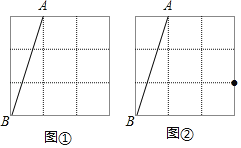
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张准备给长方形客厅铺设瓷砖,已知客厅长AB=8m,宽BC=6m,现将其划分成一个长方形EFGH区域I和环形区域Ⅱ,区域Ⅰ用甲、乙瓷砖铺设,其中甲瓷砖铺设成的是两个全等的菱形图案,区域Ⅱ用丙瓷砖铺设,如图所示,已知N是GH中点,点M在边HE上,HN=3HM,设HM=x(m).
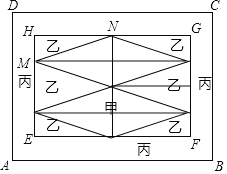
(1)用含x的代数式表示以下数量.铺设甲瓷砖的面积为 m2,铺设丙瓷砖的面积为 m2.
(2)若甲、乙、丙瓷砖单价分别为300元/m2,200元/m2,100元/m2,且EF≥FG+2,铺设好整个客厅,三种瓷砖总价至少需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
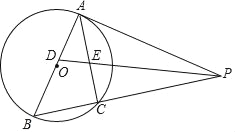
【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
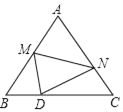
【题目】如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)从袋中任意摸出一球,放回摇匀后,再摸出一球,则两次都摸到白球的概率是多少?请你用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
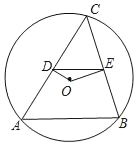
【题目】如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“特色大丰,美好生活”, 大丰区举行金色秋天旅游活动.明明和华华同学分析网上关于旅游活动的信息,发现最具特色的景点有:①荷兰花海、②梅花弯、③麋鹿保护区.他们准备周日下午去参观游览,各自在这三个景点任选一个,每个景点被选中的可能性相同.
(1)明明同学在三个备选景点中选中荷兰花海的概率是 .
(2)用树状图或列表法求出明明和华华他们选中不同景点参观的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com