
【题目】已知![]() 的直径为10cm,AB,CD是
的直径为10cm,AB,CD是![]() 的两条弦,
的两条弦,![]() ,
,![]() ,
,![]() ,则弦AB和CD之间的距离是______cm.
,则弦AB和CD之间的距离是______cm.
【答案】7或1
【解析】
分两种情况考虑:当两条弦位于圆心O一侧时,如图1所示,过O作![]() ,交CD于点F,交AB于点E,连接OA,OC,由
,交CD于点F,交AB于点E,连接OA,OC,由![]() ,得到
,得到![]() ,利用垂径定理得到E与F分别为CD与AB的中点,在直角三角形AOF中,利用勾股定理求出OF的长,在三角形COE中,利用勾股定理求出OE的长,由
,利用垂径定理得到E与F分别为CD与AB的中点,在直角三角形AOF中,利用勾股定理求出OF的长,在三角形COE中,利用勾股定理求出OE的长,由![]() 即可求出EF的长;当两条弦位于圆心O两侧时,如图2所示,同理由
即可求出EF的长;当两条弦位于圆心O两侧时,如图2所示,同理由![]() 求出EF的长即可.
求出EF的长即可.
解:分两种情况考虑:
当两条弦位于圆心O一侧时,如图1所示,
过O作![]() ,交AB于点E,交CD于点F,连接OA,OC,
,交AB于点E,交CD于点F,连接OA,OC,
![]() ,
,![]() ,
,
![]() 、F分别为AB、CD的中点,
、F分别为AB、CD的中点,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
则![]() ;
;
当两条弦位于圆心O两侧时,如图2所示,同理可得![]() ,
,
综上,弦AB与CD的距离为7cm或1cm.
故答案为:7或1.


科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
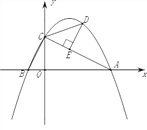
【题目】已知直线y=-![]() x+2与x轴、y轴分别交于点A、C,抛物线y=-
x+2与x轴、y轴分别交于点A、C,抛物线y=-![]() x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作
x2+bx+c过点A、C,且与x轴交于另一点B,在第一象限的抛物线上任取一点D,分别连接CD、AD,作![]() 于点E.
于点E.
(1)求抛物线的表达式;
(2)求△ACD面积的最大值;
(3)若△CED与△COB相似,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
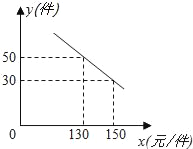
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:(1)求出y与x之间的函数关系式;(2)如果商店销售这种商品,每天要获得1500元利润,那么每件商品的销售价应定为多少元?(3)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
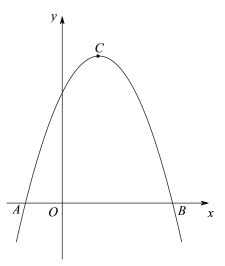
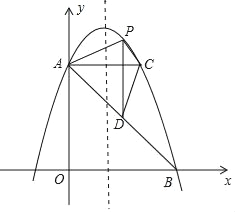
【题目】如图,在平面直角坐标系xOy中,二次函数![]() (a、b都是常数,且a<0)的图像与x轴交于点
(a、b都是常数,且a<0)的图像与x轴交于点![]() 、
、![]() ,顶点为点C.
,顶点为点C.
(1)求这个二次函数的解析式及点C的坐标;
(2)过点B的直线![]() 交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
(3)点P为抛物线上一个动点,当∠PBA=∠CBD时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
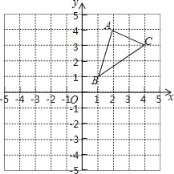
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;并写出A1、B1、C1三点的坐标.
(2)求出(1)中C点旋转到C1点所经过的路径长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与y轴交于点A,与x轴交于点B.抛物线y=﹣x2+bx+c过A、B两点.
(1)写出点A,B的坐标;
(2)求抛物线的解析式;
(3)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一动点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣3x>0.
解:设x2﹣3x=0,解得:x1=0,x2=5.则抛物线y=x2﹣3x与x轴的交点坐标为(0,0)和(3,0).画出二次函数y=x2﹣3x的大致图象(如图所示),由图象可知:当x<0或x>3时函数图象位于x轴上方,此时y>0,即x2﹣3x>0,所以,一元二次不等式x2﹣3x>0的解集为:x<0或x>3.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解答过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想 ④整体思想
(2)一元二次不等式x2﹣3x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣3x﹣4<0的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com