
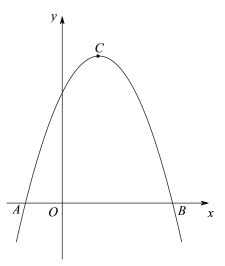
【题目】如图,在平面直角坐标系xOy中,二次函数![]() (a、b都是常数,且a<0)的图像与x轴交于点
(a、b都是常数,且a<0)的图像与x轴交于点![]() 、
、![]() ,顶点为点C.
,顶点为点C.
(1)求这个二次函数的解析式及点C的坐标;
(2)过点B的直线![]() 交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
(3)点P为抛物线上一个动点,当∠PBA=∠CBD时,求点P的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)由点A,B的坐标,利用待定系数法即可求出二次函数的解析式,再利用配发法即可求出顶点C的坐标;
(2)利用一次函数图象上点的坐标特征可求出点D的坐标,过点D作DE⊥BC,垂足为点E,设抛物线对称轴与x轴的交点为点F,由点B,C,D,F的坐标可得出CD,DF,BF的长,利用勾股定理可得出BC的长,利用角的正切值不变可求出DE的长,进而可求出BE的长,再利用余切的定义即可求出∠CBD的余切值;
(3)设直线PB与y轴交于点M,由∠PBA=∠CBD及∠CBD的余切值可求出OM的长,进而可得出点M的坐标,由点B,M的坐标,利用待定系数法即可求出直线BP的解析式,联立直线BP及二次函数解析式成方程组,通过解方程组可求出点P的坐标.
(1)将A(-2,0),B(6,0)代入y=ax2+bx+6,得:![]() ,
,
解得: ,
,
∴二次函数的解析式为y=-![]() x2+2x+6,
x2+2x+6,
∵y=-![]() x2+2x+6=-
x2+2x+6=-![]() (x-2)2+8,
(x-2)2+8,
∴点C的坐标为(2,8);、
(2)当x=2时,y=-![]() x+3=2,
x+3=2,
∴点D的坐标为(2,2),
过点D作DE⊥BC,垂足为点E,设抛物线对称轴与x轴的交点为点F,如图1所示.
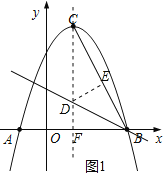
∵抛物线的顶点坐标为(2,8),
∴点F的坐标为(2,0),
∵点B的坐标为(6,0),
∴CF=8,CD=6,DF=2,BF=4,BC=![]() =4
=4![]() ,BD=
,BD=![]() =2
=2![]() ,
,
∴sin∠BCF=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴DE=![]() ,
,
∴BE=![]() =
=![]() ,
,
∴cot∠CBD=![]() =
=![]() =
=![]() ;
;
(3)设直线PB与y轴交于点M,如图2所示.
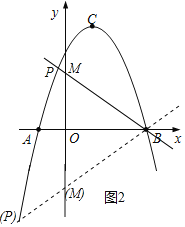
∵∠PBA=∠CBD,
∴cot∠PBA=![]() ,即
,即![]() ,
,
∴OM=![]() ,
,
∴点M的坐标为(0,![]() )或(0,-
)或(0,-![]() ),
),
设直线BP的解析式为y=mx+n(m≠0),
将B(6,0),M(0,![]() )代入y=mx+n,得:
)代入y=mx+n,得: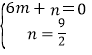 ,
,
解得: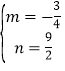 ,
,
∴直线BP的解析式为y=-![]() x+
x+![]() ,
,
同理,当点M的坐标为(0,-![]() )时,直线BP的解析式为y=-
)时,直线BP的解析式为y=-![]() x+
x+![]() ,
,
联立直线BP与抛物线的解析式成方程组,得: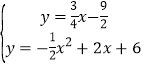 或
或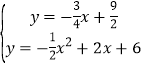 ,
,
解得: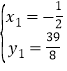 ,
,![]() 或
或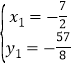 ,
,![]() ,
,
∴点P的坐标为(-![]() ,
,![]() )或(-
)或(-![]() ,-
,-![]() ).
).


科目:初中数学 来源: 题型:
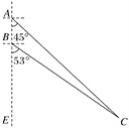
【题目】如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin 53°≈![]() ,cos 53°≈
,cos 53°≈![]() ,tan 53°≈
,tan 53°≈![]() ,
,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进我市生态文明建设,某校在美化校园活动中,设计小组想借助如图所示的直角墙角(两边足够长),用30m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为216m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和8m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
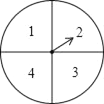
【题目】如图,有一个可以自由转动的转盘被平均分成4个扇形,分别标有1、2、3、4四个数字,小王和小李各转动一次转盘为一次游戏.当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;(2)求每次游戏结束得到的一组数恰好是方程x2﹣4x+3=0的解的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论(1)4a+2b+c>0;(2)方程ax2+bx+c=0两根之和小于零;(3)y随x的增大而增大;(4)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数是( )
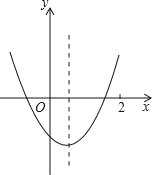
A. 4 个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y.
(1)计算由x、y确定的点(x,y)在函数y=﹣x+6图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com