
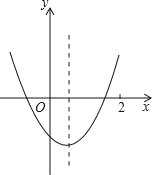
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论(1)4a+2b+c>0;(2)方程ax2+bx+c=0两根之和小于零;(3)y随x的增大而增大;(4)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数是( )
A. 4 个B. 3个C. 2个D. 1个
【答案】D
【解析】
根据函数的图象可知x=2时,函数值的正负性,即可对(1)作出判断;根据函数图象的开口方向得出a的符号,根据对称轴在y轴右侧可得出b的符号,根据图象与y轴的交点可得出c的符号,根据一元二次方程根与系数的关系即可对(2)作出判断;二次函数的增减性需要找到其对称轴才知具体情况,故(3)错误;根据b、c的符号即可得出一次函数y=x+bc所经过的象限进而对(4)作出判断.
解:∵当x=2时,y=4a+2b+c,由图象可知当x=2时对应的点在x轴的上方,即4a+2b+c>0;故(1)正确;
由二次函数y=ax2+bx+c(a≠0)的图象可知:图象开口向上,a>0,对称轴在y轴右侧,![]() >0,所以b<0,图象与y轴交在负半轴,c<0,所以一元二次方程ax2+bx+c =0的两根之和为
>0,所以b<0,图象与y轴交在负半轴,c<0,所以一元二次方程ax2+bx+c =0的两根之和为![]() >0,故(2)错误;
>0,故(2)错误;
因为函数的增减性需要找到其对称轴才知具体情况,不能在整个自变量取值范围内说y随x的增大而增大,故(3)错误;
因为c<0,b<0,
所以bc>0,
所以一次函数y=x+bc的图象一定经过第二象限,故(4)错误.
所以正确的个数是1个.
故选:D.


科目:初中数学 来源: 题型:
【题目】请从下列两个小题中任选一个作答,若多选,则按第一题计分.
A:一个正多边形的一个外角为36°,则这个多边形的对角线有_____条.
B:在△ABC中AB=AC,若AB=3,BC=4,则∠A的度数约为_____.(用科学计算器计算,结果精确到0.1°.)
查看答案和解析>>
科目:初中数学 来源: 题型:
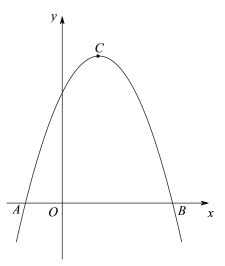
【题目】如图,在平面直角坐标系xOy中,二次函数![]() (a、b都是常数,且a<0)的图像与x轴交于点
(a、b都是常数,且a<0)的图像与x轴交于点![]() 、
、![]() ,顶点为点C.
,顶点为点C.
(1)求这个二次函数的解析式及点C的坐标;
(2)过点B的直线![]() 交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
(3)点P为抛物线上一个动点,当∠PBA=∠CBD时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
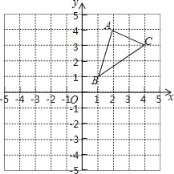
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;并写出A1、B1、C1三点的坐标.
(2)求出(1)中C点旋转到C1点所经过的路径长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
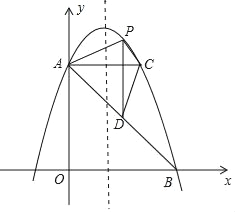
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与y轴交于点A,与x轴交于点B.抛物线y=﹣x2+bx+c过A、B两点.
(1)写出点A,B的坐标;
(2)求抛物线的解析式;
(3)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一动点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D在边AC上,BD的垂直平分线交CA的延长线于点E,交BD于点F,联结BE,ED2=EAEC.
(1)求证:∠EBA=∠C;
(2)如果BD=CD,求证:AB2=ADAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
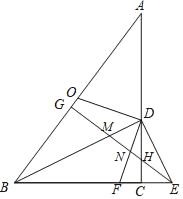
【题目】在△ABC中,∠ACB=90°,BC=3,AC=4,点O是AB的中点,点D是边AC上一点,DE⊥BD,交BC的延长线于点E,OD⊥DF,交BC边于点F,过点E作EG⊥AB,垂足为点G,EG分别交BD、DF、DC于点M、N、H.
(1)求证:![]() ;
;
(2)设CD=x,NE=y,求y关于x的函数关系式及其定义域;
(3)当△DEF是以DE为腰的等腰三角形时,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
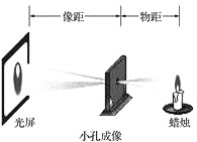
【题目】两千多年前,我国的学者墨子和他的学生做了小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小华在学习了小孔成像的原理后,利用如图装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20 cm,光屏在距小孔30 cm处,小华测量了蜡烛的火焰高度为2 cm,则光屏上火焰所成像的高度为__________ cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com