
【题目】请从下列两个小题中任选一个作答,若多选,则按第一题计分.
A:一个正多边形的一个外角为36°,则这个多边形的对角线有_____条.
B:在△ABC中AB=AC,若AB=3,BC=4,则∠A的度数约为_____.(用科学计算器计算,结果精确到0.1°.)
科目:初中数学 来源: 题型:
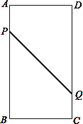
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿以2cm/s的速度向点D移动.经过多长时间P、Q两点的距离是10?
查看答案和解析>>
科目:初中数学 来源: 题型:
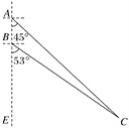
【题目】如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin 53°≈![]() ,cos 53°≈
,cos 53°≈![]() ,tan 53°≈
,tan 53°≈![]() ,
,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
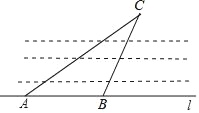
【题目】如图,已知公路l上A、B两点之间的距离为50m,小明要测量点C与河对岸边公路l的距离,测得∠ACB=∠CAB=30°.点C到公路l的距离为( )
A. 25m B. ![]() m C. 25
m C. 25![]() m D. (25+25
m D. (25+25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
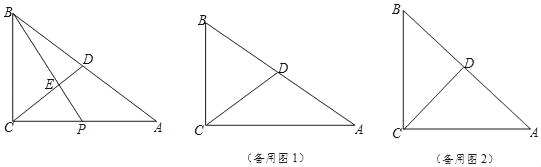
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cosA的值;
(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
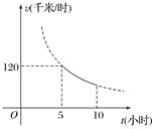
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进我市生态文明建设,某校在美化校园活动中,设计小组想借助如图所示的直角墙角(两边足够长),用30m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为216m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和8m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论(1)4a+2b+c>0;(2)方程ax2+bx+c=0两根之和小于零;(3)y随x的增大而增大;(4)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数是( )
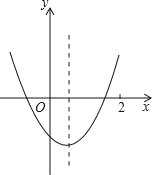
A. 4 个B. 3个C. 2个D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com