
【题目】如图二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() 、
、![]() ,交
,交![]() 轴于
轴于![]() ,直线
,直线![]() 平行于
平行于![]() 周,与抛物线另一个交点为
周,与抛物线另一个交点为![]() .
.
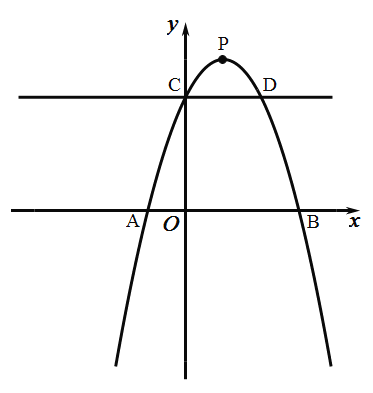
(1)求函数的解析式;
(2)若![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 是抛物线上的动点,求使以
是抛物线上的动点,求使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形的
为顶点的四边形是平行四边形的![]() 的横坐标.
的横坐标.
【答案】(1)![]() ;(2)1或
;(2)1或![]() 或
或![]() 或5.
或5.
【解析】
(1)先设二次函数的解析式为![]() ,展开得
,展开得![]() ,
,
再把![]() 代入,求出a的值即可;
代入,求出a的值即可;
(2)先联立方程组![]() ,求出
,求出![]() 点坐标为
点坐标为![]() ,当以
,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点四边形是平行四边形时,有两种情况讨论,
为顶点四边形是平行四边形时,有两种情况讨论,![]() 是平行四边形的边时和
是平行四边形的边时和![]() 是平行四边形的对角线时,分别求解即可.
是平行四边形的对角线时,分别求解即可.
解:(1)![]() 二次函数的图像交
二次函数的图像交![]() 轴于
轴于![]() 、
、![]() ,
,
![]() 设二次函数的解析式为
设二次函数的解析式为![]()
展开得:![]() ,
,
![]() 二次函数的图像交
二次函数的图像交![]() 轴于
轴于![]() ,
,
![]() ,得
,得![]()
![]() 二次函数的解析式为
二次函数的解析式为![]()
(2)联立方程组得:![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点四边形是平行四边形时,有两类情形;
为顶点四边形是平行四边形时,有两类情形;
①![]() 是平行四边形的边时,
是平行四边形的边时,
联立方程组![]() ,
,
解得,![]()
如图,此时![]() ,或
,或![]() 或
或![]()
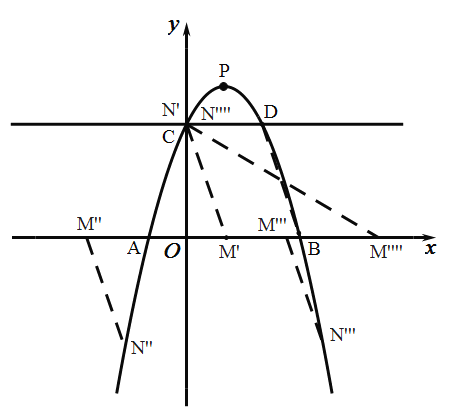
②![]() 是平行四边形的对角线时
是平行四边形的对角线时
![]() 、
、![]() 两点的中点坐标为
两点的中点坐标为![]() ,
,
![]() 设
设![]() ,可得
,可得![]() 的坐标为
的坐标为![]() ,
,
将![]() 的坐标
的坐标![]() 代入
代入![]() ,
,
得![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
得![]()


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,![]() 内接于
内接于![]() ,AD是直径,
,AD是直径,![]() 的平分线交BD于H,交
的平分线交BD于H,交![]() 于点C,连接DC并延长,交AB的延长线于点E.
于点C,连接DC并延长,交AB的延长线于点E.
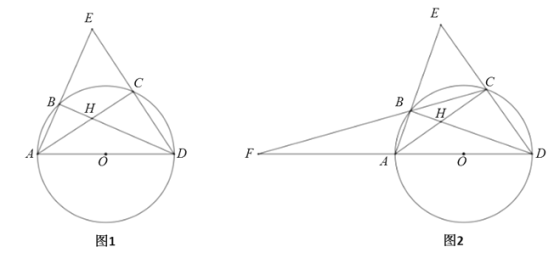
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值
的值
(3)如图2,连接CB并延长,交DA的延长线于点F,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
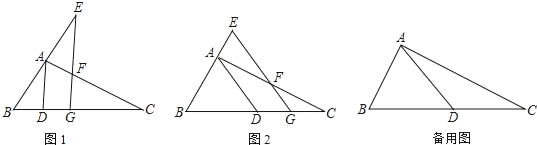
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
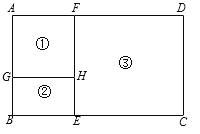
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,关于x的方程:x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() 的解是x1=c,x2=﹣
的解是x1=c,x2=﹣![]() ;x+
;x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;……
;……
(1)请观察上述方程与解的特征,比较关于x的方程x+![]() =c+
=c+![]() (a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.
(a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.
(2)可以直接利用(1)的结论,解关于x的方程:x+![]() =a+
=a+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
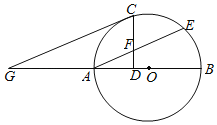
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若sinG=0.6,CF=4,求GA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=10,高AD=8,M、N、P分别在边AB、BC、AC上移动,但不与A、B、C重合,连接MN、NP、MP,且MP始终与BC保持平行,AD与MP相交于点E,设MP=x,△MNP的面积用y表示.
(1)求y关于x的函数关系式;
(2)当x取什么值时,y有最大值,并求出的最大值;
(3)当x取什么值时,△MNP是等腰直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
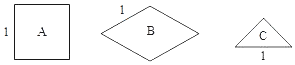
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com