
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌОЙ§CЃЈ1ЃЌ1ЃЉЕФХзЮяЯпyЃНax2+bx+cЃЈaЃО0ЃЉЖЅЕуЮЊMЃЌгыxжсе§АыжсНЛгкAЃЌBСНЕуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгOCЃЌНЋЯпЖЮOCШЦЕуOФцЪБеыа§зЊЪЙЕУCТфдкyжсЕФе§АыжсЩЯЃЌЧѓЯпЖЮOCЙ§ЕФУцЛ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌбгГЄЯпЖЮOCжСNЃЌЪЙЕУONЃН![]() OCЃЌШєЁЯONAЃНЁЯOBNЧвtanЁЯBAMЃН
OCЃЌШєЁЯONAЃНЁЯOBNЧвtanЁЯBAMЃН![]() ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌвбжЊвджБЯпxЃН![]() ЮЊЖдГЦжсЕФХзЮяЯпyЃНax2+bx+cНЛyжсгкЃЈ0ЃЌ5ЃЉЃЌНЛжБЯпlЃКyЃНkx+mЃЈkЃО0ЃЉгкCЃЌDСНЕуЃЌШєдкxжсЩЯгаЧвНігавЛЕуPЃЌЪЙЁЯCPDЃН90ЁуЃЌЧѓkЕФжЕЃЎ
ЮЊЖдГЦжсЕФХзЮяЯпyЃНax2+bx+cНЛyжсгкЃЈ0ЃЌ5ЃЉЃЌНЛжБЯпlЃКyЃНkx+mЃЈkЃО0ЃЉгкCЃЌDСНЕуЃЌШєдкxжсЩЯгаЧвНігавЛЕуPЃЌЪЙЁЯCPDЃН90ЁуЃЌЧѓkЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉyЃН2x2Љ9x+8ЃЛЃЈ3ЃЉkЃН
ЃЛЃЈ2ЃЉyЃН2x2Љ9x+8ЃЛЃЈ3ЃЉkЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯпЖЮOCЙ§ЕФУцЛ§ЃН![]() ЁСІаЁСЃЈ
ЁСІаЁСЃЈ![]() ЃЉ2ЃН
ЃЉ2ЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁїONAЁзЁїOBNЃЌдђOAOBЃНON2ЃН4ЃЌМДmnЃН4ЁЂйЃЌдђХзЮяЯпЕФБэДяЪНЮЊЃКyЃНaЃЈxЉmЃЉЃЈxЉnЃЉЃЌMHЃН|yM|ЃНЉaЃЈ![]() ЉmЃЉЃЈ
ЉmЃЉЃЈ![]() ЉnЃЉЃН
ЉnЃЉЃН![]() ЃЌAHЈT
ЃЌAHЈT![]() ЉmЃЌtanЁЯBAMЃН
ЉmЃЌtanЁЯBAMЃН![]() ЃН
ЃН![]() aЃЈnЉmЃЉЃН
aЃЈnЉmЃЉЃН![]() ЃЌЛЏМђЕУЃКaЃЈnЉmЃЉЃН
ЃЌЛЏМђЕУЃКaЃЈnЉmЃЉЃН![]() ЁЂкЃЌНЋЃЈ1ЃЌ1ЃЉДњШыyЃНaЃЈxЉmЃЉЃЈxЉnЃЉВЂЛЏМђЕУЃКaЃЈ5ЉmЉnЃЉЃН1ЁЂлЃЌСЊСЂЂйЂкЂлМДПЩЧѓНтЃЛ
ЁЂкЃЌНЋЃЈ1ЃЌ1ЃЉДњШыyЃНaЃЈxЉmЃЉЃЈxЉnЃЉВЂЛЏМђЕУЃКaЃЈ5ЉmЉnЃЉЃН1ЁЂлЃЌСЊСЂЂйЂкЂлМДПЩЧѓНтЃЛ
ЃЈ3ЃЉХзЮяЯпЕФБэДяЪНЮЊЃКyЃНx2Љ5x+5ЃЛЩшЕуDЃЈmЃЌnЃЉЃЌnЃНm2Љ5m+5ЃЌЖјЕуCЃЈ1ЃЌ1ЃЉЃЌдђkЃН![]() ЃНmЉ4ЃЌШєдкxжсЩЯгаЧвНігавЛЕуPЃЌЪЙЁЯCPDЃН90ЁуЃЌдђЙ§CDжаЕуЕФдВRгыxжсЯрЧаЃЌМДПЩЧѓНтЃЎ
ЃНmЉ4ЃЌШєдкxжсЩЯгаЧвНігавЛЕуPЃЌЪЙЁЯCPDЃН90ЁуЃЌдђЙ§CDжаЕуЕФдВRгыxжсЯрЧаЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЯпЖЮOCЙ§ЕФУцЛ§ЃН![]() ЁСІаЁСЃЈ
ЁСІаЁСЃЈ![]() ЃЉ2ЃН
ЃЉ2ЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉONЃН![]() OCЃН4ЃЌЩшЕуAЁЂBЕФзјБъЗжБ№ЮЊЃКЃЈmЃЌ0ЃЉЁЂЃЈnЃЌ0ЃЉЃЌ
OCЃН4ЃЌЩшЕуAЁЂBЕФзјБъЗжБ№ЮЊЃКЃЈmЃЌ0ЃЉЁЂЃЈnЃЌ0ЃЉЃЌ
ЁЯONAЃНЁЯOBNЃЌдђЁїONAЁзЁїOBNЃЌдђOAOBЃНON2ЃН4ЃЌМДmnЃН4ЁЂйЃЌ
дђХзЮяЯпЕФБэДяЪНЮЊЃКyЃНaЃЈxЉmЃЉЃЈxЉnЃЉЃЌ
Й§ЕуMзїMHЁЭABНЛABгкЕуHЃЌКЏЪ§ЕФЖдГЦжсЮЊЃКxЃН![]() ЃЈm+nЃЉЃЌ
ЃЈm+nЃЉЃЌ
дђMHЃН|yM|ЃНЉaЃЈ![]() ЉmЃЉЃЈ
ЉmЃЉЃЈ![]() ЉnЃЉЃН
ЉnЃЉЃН![]() ЃЌ
ЃЌ
AHЃНxMЉxAЃН![]() Љm
Љm
tanЁЯBAMЃН![]() ЃН
ЃН![]() aЃЈnЉmЃЉЃН
aЃЈnЉmЃЉЃН![]() ЃЌ
ЃЌ
ЛЏМђЕУЃКaЃЈnЉmЃЉЃН![]() ЁЂкЃЌ
ЁЂкЃЌ
НЋЃЈ1ЃЌ1ЃЉДњШыyЃНaЃЈxЉmЃЉЃЈxЉnЃЉВЂЛЏМђЕУЃКaЃЈ5ЉmЉnЃЉЃН1ЁЂлЃЌ
СЊСЂЂйЂкЂлВЂНтЕУЃКmЃН![]() ЃЌnЃН
ЃЌnЃН![]() ЃЌaЃН2ЃЌ
ЃЌaЃН2ЃЌ
дђХзЮяЯпЕФБэДяЪНЮЊyЃНaЃЈxЉmЃЉЃЈxЉnЃЉЃНaЃЈx2ЉmxЉnx+mnЃЉЃН2x2Љ9x+8ЃЛ
ЃЈ3ЃЉгЩЬтвтЕУЃК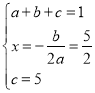 ЃЌНтЕУЃК
ЃЌНтЕУЃК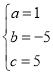 ЃЌ
ЃЌ
ЙЪХзЮяЯпЕФБэДяЪНЮЊЃКyЃНx2Љ5x+5ЃЛ
ЩшЕуDЃЈmЃЌnЃЉЃЌnЃНm2Љ5m+5ЃЌЖјЕуCЃЈ1ЃЌ1ЃЉЃЌ
дђkЃН![]() ЃНmЉ4ЃЌ
ЃНmЉ4ЃЌ
ШєдкxжсЩЯгаЧвНігавЛЕуPЃЌЪЙЁЯCPDЃН90ЁуЃЌдђЙ§CDжаЕуЕФдВRгыxжсЯрЧаЃЌЩшЧаЕуЮЊPЃЌ
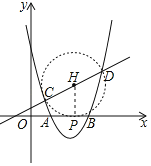
дђЕуHЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдђHPЃНHCЃЌ
ЃЉЃЌдђHPЃНHCЃЌ
МДЃЈ![]() Љ1ЃЉ2+ЃЈ
Љ1ЃЉ2+ЃЈ![]() Љ1ЃЉ2ЃНЃЈ
Љ1ЃЉ2ЃНЃЈ![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЛЏМђЕУЃК3m2Љ18m+19ЃН0ЃЌ
НтЕУЃКmЃН3+![]() ЃЈВЛКЯЬтвтЕФжЕвбЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЕФжЕвбЩсШЅЃЉЃЌ
kЃНmЉ4ЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпyЃНЉx2+2x+8гыxжсНЛгкBЁЂCСНЕуЃЌЕуDЦНЗжBCЃЌЧвЕуAЮЊХзЮяЯпЩЯЕФЕуЃЌЧвЁЯBACЮЊШёНЧЃЌдђADЕФжЕЗЖЮЇЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФДќзгРяга1ИіКьЧђКЭnИіАзЧђЃЌЫќУЧГ§беЩЋЭтЦфгрЖМЯрЭЌЃЎ
ЃЈ1ЃЉДгетИіДќзгРяУўГівЛИіЧђЃЌМЧТМЦфбеЩЋЃЌШЛКѓЗХЛиЃЌвЁОљдШКѓЃЌжиИДИУЪЕбщЃЌОЙ§ДѓСПЪЕбщКѓЃЌЗЂЯжУўЕНАзЧђЕФЦЕТЪЮШЖЈгк![]() зѓгвЃЌЧѓnЕФжЕЃЛ
зѓгвЃЌЧѓnЕФжЕЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЯШДгетИіДќжаУўГівЛИіЧђЃЌМЧТМЦфбеЩЋЃЌЗХЛиЃЌвЁОљдШКѓЃЌдйДгДќжаУўГівЛИіЧђЃЌМЧТМЦфбеЩЋЃЎЧыгУЛЪїзДЭМЛђепСаБэЕФЗНЗЈЃЌЧѓГіЯШКѓСНДЮУўГіВЛЭЌбеЩЋЕФСНИіЧђЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгквЛИіКЏЪ§ЃЌШчЙћЫќЕФздБфСП x гыКЏЪ§жЕ y ТњзуЃКЕБ1ЁмxЁм1 ЪБЃЌ1ЁмyЁм1ЃЌдђГЦетИіКЏЪ§ЮЊЁАБе КЏЪ§ЁБ.Р§ШчЃКy=xЃЌy=x ОљЪЧЁАБеКЏЪ§ЁБ. вбжЊ y ax2 bx c(a0) ЪЧЁАБеКЏЪ§ЁБЃЌЧвХзЮяЯпОЙ§Еу A(1ЃЌ1)КЭЕу B(1ЃЌ1)ЃЌдђ a ЕФШЁжЕЗЖЮЇЪЧ______________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫИјгЮПЭЬсЙЉИќКУЕФЗўЮёЃЌФГОАЧјЫцЛњЖдВПЗжгЮПЭНјааСЫЙигкЁАОАЧјЗўЮёЙЄзїТњвтЖШЁБЕФЕїВщЃЌВЂИљОнЕїВщНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМБэ.
ТњвтЖШ | ШЫЪ§ | ЫљеМАйЗжБШ |
ЗЧГЃТњвт | 12 | 10% |
Тњвт | 54 | m |
БШНЯТњвт | n | 40% |
ВЛТњвт | 6 | 5% |

ИљОнЭМБэаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
(1)БОДЮЕїВщЕФзмШЫЪ§ЮЊ______ЃЌБэжаmЕФжЕЮЊ_______ЃЛ
(2)ЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
(3)ОнЭГМЦЃЌИУОАЧјЦНОљУПЬьНгД§гЮПЭдМ3600ШЫЃЌШєНЋЁАЗЧГЃТњвтЁБКЭЁАТњвтЁБзїЮЊгЮПЭЖдОАЧјЗўЮёЙЄзїЕФПЯЖЈЃЌЧыФуЙРМЦИУОАЧјЗўЮёЙЄзїЦНОљУПЬьЕУЕНЖрЩйУћгЮПЭЕФПЯЖЈ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкжНУцЩЯгавЛЪ§жсЃЈШчЭМЃЉЃЌелЕўжНУцЃЎ
ЃЈ1ЃЉШє1БэЪОЕФЕугыЉ1БэЪОЕФЕужиКЯЃЌдђЉ3БэЪОЕФЕугыЪ§ЁЁ ЁЁБэЪОЕФЕужиКЯЃЛ
ЃЈ2ЃЉШєЉ1БэЪОЕФЕугы3БэЪОЕФЕужиКЯЃЌЛиД№вдЯТЮЪЬтЃК
ЂйдЕугыЪ§ЁЁ ЁЁБэЪОЕФЕужиКЯЃЛ
ЂкШєЪ§жсЩЯAЁЂBСНЕужЎМфЕФОрРыЮЊ7ЃЌЧвAЁЂBСНЕуОелЕўКѓжиКЯЃЌдђAЁЂBСНЕуБэЪОЕФЪ§ЪЧЁЁ ЁЁ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧ![]() ЕФжБОЖЃЌACЮЊЯвЃЌ
ЕФжБОЖЃЌACЮЊЯвЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкЕуDЃЌЙ§ЕуDЕФЧаЯпНЛACЕФбгГЄЯпгкЕуEЃЎ
гкЕуDЃЌЙ§ЕуDЕФЧаЯпНЛACЕФбгГЄЯпгкЕуEЃЎ
ЧѓжЄЃК![]() ЃЛ
ЃЛ
![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНкдМгУЫЎЃЌФГЫЎГЇЙцЖЈЃКФГЕЅдЊОгУёШчЙћвЛИідТЕФгУЫЎСПВЛГЌЙ§![]() ЖжЃЌФЧУДетИідТИУЕЅдЊОгУёжЛНЛ10дЊЫЎЗбЃЎШчЙћГЌЙ§
ЖжЃЌФЧУДетИідТИУЕЅдЊОгУёжЛНЛ10дЊЫЎЗбЃЎШчЙћГЌЙ§![]() ЖжЃЌдђетИідТГ§СЫШдвЊНЛ10дЊЫЎЗбЭтЃЌГЌЙ§ФЧВПЗжАДУПЖж
ЖжЃЌдђетИідТГ§СЫШдвЊНЛ10дЊЫЎЗбЭтЃЌГЌЙ§ФЧВПЗжАДУПЖж![]() дЊНЛЗбЃЎ
дЊНЛЗбЃЎ
ЃЈ1ЃЉИУЕЅдЊОгУё8дТЗнгУЫЎ80ЖжЃЌГЌЙ§СЫЁАЙцЖЈЕФ![]() ЖжЁБЃЌдђГЌЙ§ВПЗжгІНЛЫЎЗб ЃЈ80-xЃЉ
ЖжЁБЃЌдђГЌЙ§ВПЗжгІНЛЫЎЗб ЃЈ80-xЃЉ
дЊЃЈгУКЌxЕФЪНзгБэЪОЃЉЃЎ
ЃЈ2ЃЉЯТБэЪЧИУЕЅдЊОгУё9дТЁЂ10дТЕФгУЫЎЧщПіКЭНЛЗбЧщПіЃК
дТЗн | гУЫЎСПЃЈЖжЃЉ | НЛЗбзмЪ§ЃЈдЊЃЉ |
9дТЗн | 85 | 25 |
10дТЗн | 50 | 10 |
ИљОнЩЯБэЪ§ОнЃЌЧѓИУxЖжЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
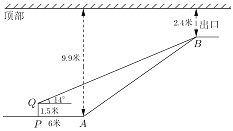
ЁОЬтФПЁПЕиЬњ10КХЯпФГеОЕуГіПкКсНиУцЦНУцЭМШчЭМЫљЪОЃЌЕчЬн![]() ЕФСНЖЫЗжБ№ОрЖЅВП9.9УзКЭ2.4УзЃЌдкОрЕчЬнЦ№Еу
ЕФСНЖЫЗжБ№ОрЖЅВП9.9УзКЭ2.4УзЃЌдкОрЕчЬнЦ№Еу![]() ЖЫ6УзЕФ
ЖЫ6УзЕФ![]() ДІЃЌгУ1.5УзЕФВтНЧвЧВтЕУЕчЬнжеЖЫ
ДІЃЌгУ1.5УзЕФВтНЧвЧВтЕУЕчЬнжеЖЫ![]() ДІЕФбіНЧЮЊ14ЁуЃЌЧѓЕчЬн
ДІЕФбіНЧЮЊ14ЁуЃЌЧѓЕчЬн![]() ЕФЦТЖШгыГЄЖШ.ЃЈВЮПМЪ§ОнЃК
ЕФЦТЖШгыГЄЖШ.ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com