
 (1)已知⊙O的直径为6,圆心O到直线l的距离为5,
(1)已知⊙O的直径为6,圆心O到直线l的距离为5,分析 (1)①根据圆心距和两圆半径的之间关系可得出两圆之间的位置关系;
②点P到直线l的距离的最大值=圆心O到直线l的距离+⊙O的半径,最小值=圆心O到直线l的距离-⊙O的半径;
(2)如图,连接OC;首先证明CE=DE;其次运用勾股定理求出CE的长,即可解决问题.
解答 解:(1)①∵⊙O的直径为6,
∴⊙O的半径为3,
∵圆心O到直线l的距离是5,5>3,
∴直线l与⊙O的位置关系是相离;
②点P到直线l的距离的最大值=5+6÷2=8,最小值=5-6÷2=2;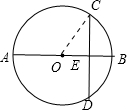 (2)如图,连接OC;
(2)如图,连接OC;
∵直径AB=10,BE=2,
∴OE=5-2=3,OC=5;
∵弦CD⊥AB,
∴CE=DE;
由勾股定理得:
CE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴CD=2CE=8.
故答案为:相离.
点评 此题考查了由数量关系来判断两圆位置关系的方法.设两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.考查了勾股定理、垂径定理等几何知识点及其应用问题;解题的关键是作辅助线,灵活运用勾股定理、垂径定理等几何知识点来分析、判断、求解.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )| A. | (3,4) | B. | (4,4) | C. | (7,3) | D. | (7,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分点,下列作法正确的是( )
如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分点,下列作法正确的是( )| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′为AC延长线上一点,A′是B′B延长线上一点,且△A′B′C≌△ABC,则∠BCA′:∠BCB′=1:4.
如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′为AC延长线上一点,A′是B′B延长线上一点,且△A′B′C≌△ABC,则∠BCA′:∠BCB′=1:4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABE和△ACD中,给出以下4个论断:
如图所示,在△ABE和△ACD中,给出以下4个论断:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水果销售店在试销售成本为每千克2元的某种水果,规定试销期间销售单价不低于成本单价,也不高于每千克4元.经试销发现,每天的销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
某水果销售店在试销售成本为每千克2元的某种水果,规定试销期间销售单价不低于成本单价,也不高于每千克4元.经试销发现,每天的销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com