如图，在直角坐标系中有一直角三角形AOB，O为坐标原点，OA=1．tan∠BAO=3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y=ax2+bx+c经过点A、B、C．
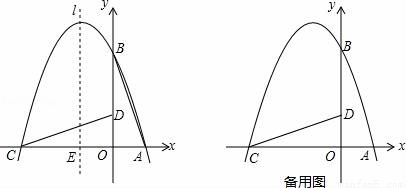
（1）求抛物线的解析式；
（2）若点P是第二象限内抛物线上的动点，其横坐标为t，
①设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求出当△CEF与△COD相似时，点P的坐标；
②是否存在一点P，使△PCD得面积最大？若存在，求出△PCD的面积的最大值；若不存在，请说明理由．
科目：初中数学 来源：2016届山东省济南市平阴县中考三模数学试卷（解析版） 题型：解答题
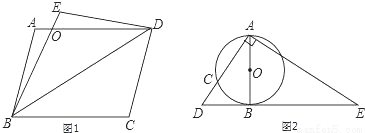
（1）如图1，在平行四边形ABCD中，将△BCD沿BD翻折，使点C落在点E处，BE和AD相交于点O．求证：OA=OE．
（2）如图2，AB是⊙O的直径，AC是⊙O的弦，过点B作⊙O的切线DE，与AC的延长线交于点D，作AE⊥AC交DE于点E．求证：∠BAD=∠E．
查看答案和解析>>
科目：初中数学 来源：2016届山东省聊城市冠县中考二模数学试卷（解析版） 题型：选择题
若不等式组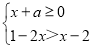
无解，则实数a的取值范围是（ ）
A．a≥-1 B．a＜-1 C．a≤1 D．a≤-1
查看答案和解析>>
科目：初中数学 来源：2016届山东省日照市莒县中考一模数学试卷（解析版） 题型：选择题
如图，正方形ABCD的边长为a，在AB、BC、CD、DA边上分别取点A1、B1、C1、D1，使AA1=BB1=CC1=DD1=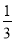
a，在边A1B1、B1C1，C1D1、D1A1上分别取点A2、B2、C2、D2，使A1A2、B1B2、C1C2、D1D2=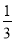A1B1，…，依次规律继续下去，则正方形AnBnCnDn的面积为（ ）
A．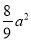
B．（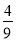
）na2 C．（
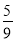）n-1a2 D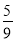．（）na2
查看答案和解析>>
科目：初中数学 来源：2016届山东省泰安市中考一模数学试卷（解析版） 题型：填空题
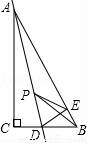
如图，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是 ．
查看答案和解析>>
科目：初中数学 来源：2016届山东省泰安市中考一模数学试卷（解析版） 题型：选择题
如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）
A．78° B．75° C．60° D．45°
查看答案和解析>>
科目：初中数学 来源：2016届山东省潍坊市寿光市5月中考模拟数学试卷（解析版） 题型：解答题
如图，抛物线y=ax2+bx+1经过点（2，6），且与直线y=
x+1相交于A，B两点，点A在y轴上，过点B作BC⊥x轴，垂足为点C（4，0）．
（1）求抛物线的解析式；
（2）若P是直线AB上方该抛物线上的一个动点，过点P作PD⊥x轴于点D，交AB于点E，求线段PE的最大值；
（3）在（2）的条件，设PC与AB相交于点Q，当线段PC与BE相互平分时，请求出点Q的坐标．
查看答案和解析>>
科目：初中数学 来源：2016届江苏省无锡市锡北片九年级下期中数学试卷（解析版） 题型：选择题
已知，如图2菱形ABCD四个顶点都在坐标轴上，对角线AC、BD交于原点O，DF垂直AB交AC于点G，反比例函数
，经过线段DC的中点E，若BD=4，则AG的长为（ ）
A．
B．
+2 C．2+1 D．
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的解集在数轴上表示为（ ）