
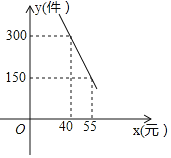
【题目】某网店销售一种文具袋,成本为30元/件,每天的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足一次函数关系,其图象如图所示.
(元)之间满足一次函数关系,其图象如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天的销量不低于240件,那么当销售单价为多少元时,每天获取的利润最大?最大利润是多少?
 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】已知如图,线段AB=60,AD=13,DE=17,EF=7,请问在D,E,F,三点中,哪一点最接近线段AB的黄金分割点( )
![]()
A.D 点B.E 点C.F点D.D 点或 F点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-2,1),B(0,4),C(8,16),O(0,0),P(m,n),抛物线y=ax2(a≠0)经过A,B,C,其中的一点,
(1)求抛物线y=ax2(a≠0)的解析式;
(2)若直线y=mx(m≠0)与直线y=nx(n≠0)分别经过点A与点C,判断点P(m,n)是否在反比例函数y=-![]() 的图象上;
的图象上;
(3)若点P(m,n)是反比例函数y=-![]() 的图象上任一点,且直线y=mx(m≠0)与直线y=nx(n≠0)分别与抛物线y=ax2(a≠0)交于点M,点N(不同于原点),求证:M,B,N三点在一条直线上.
的图象上任一点,且直线y=mx(m≠0)与直线y=nx(n≠0)分别与抛物线y=ax2(a≠0)交于点M,点N(不同于原点),求证:M,B,N三点在一条直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
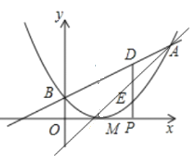
【题目】已知二次函数图象的顶点坐标为![]() ,直线
,直线![]() 与二次函数的图象交于
与二次函数的图象交于![]() ,
,![]() 两点,其中
两点,其中![]() 点的坐标为
点的坐标为![]() ,
,![]() 点在
点在![]() 轴上.
轴上.
(1)求![]() 的值及这个二次函数的解析式;
的值及这个二次函数的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的周长最小,并求出此时
的周长最小,并求出此时![]() 点坐标;
点坐标;
(3)若![]() 是
是![]() 轴上的一个动点,过
轴上的一个动点,过![]() 作
作![]() 轴的垂线分别于直线
轴的垂线分别于直线![]() 和二次函数的图象交于
和二次函数的图象交于![]() ,
,![]() 两点.当
两点.当![]() 时,求线段
时,求线段![]() 的最大值;
的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少( )个时,网球可以落入桶内.
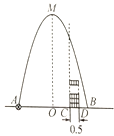
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元时,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为x(元/件),每月饰品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)如何确定售价才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制售价?
查看答案和解析>>
科目:初中数学 来源: 题型:
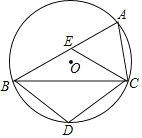
【题目】如图,△ABC是⊙O的内接三角形,点D在![]() 上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=ABAC;
(3)已知⊙O的半径为3.
①若![]() =
=![]() ,求BC的长;
,求BC的长;
②当![]() 为何值时,ABAC的值最大?
为何值时,ABAC的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com