
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元时,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为x(元/件),每月饰品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)如何确定售价才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制售价?
【答案】(1) ;
;
(2)当售价为65元时,利润最大,最大利润为6250元;
(3)将销售价格控制在55元到70元之间(含55元和70元)才能使每月利润不少于6000元.
【解析】
(1)直接根据题意售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件,进而得出等量关系;
(2)利用每件利润×销量=总利润,进而利用配方法求出即可;
(3)利用函数图象结合一元二次方程的解法得出符合题意的答案.
(1)由题意得:涨价时:y=300-(x-60)×10=-10x+900,
降价时:y=300+(60-x) ×20=-20x+1500,
即
(2)由题意可得: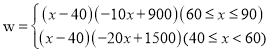 ,
,
化简得: ,
,
即 ,
,
6125<6250,
故当售价为65元时,利润最大,最大利润为6250元;
(3)令w=6000,
即6000=﹣10(x﹣65)2+6250,6000=﹣20(x-57.5)2+6125,
解得:x1=55,x2=60,x3=70,
当w≥6000时,
知:55≤x≤70,
故将销售价格控制在55元到70元之间(含55元和70元)才能使每月利润不少于6000元.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
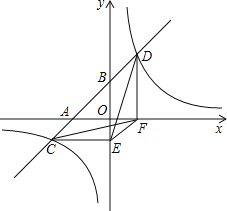
【题目】如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数y=![]() 的图象相交于C、D两点,分别过C、D两点作y轴和x轴的垂线,垂足分别为E、F,连接CF、DE.下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④tan∠BAO=a;其中正确的结论是_____.(把你认为正确结论的序号都填上)
的图象相交于C、D两点,分别过C、D两点作y轴和x轴的垂线,垂足分别为E、F,连接CF、DE.下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④tan∠BAO=a;其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)甲队队员身高的平均数为 厘米,乙队队员身高的平均数为 厘米;
(2)你认为哪支仪仗队更为整齐?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
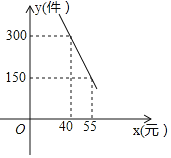
【题目】某网店销售一种文具袋,成本为30元/件,每天的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足一次函数关系,其图象如图所示.
(元)之间满足一次函数关系,其图象如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天的销量不低于240件,那么当销售单价为多少元时,每天获取的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
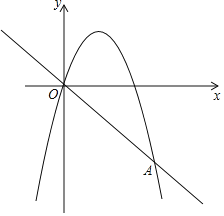
【题目】如图,已知一次函数y=﹣x与二次函数y=﹣x2+bx+c的图象相交于原点O和另一点A(4,﹣4).
(1)求二次函数表达式;
(2)直线x=m和x=m+2分别交线段AO于C、D,交二次函数y=﹣x2+bx+c的图象于点E、F,当m为何值时,四边形CEFD是平行四边形;
(3)在第(2)题的条件下,设CE与x轴的交点为M,将△COM绕点O逆时针旋转得到△C′OM′,当C′、M′、F三点第一次共线时,请画出图形并直接写出点C′的纵坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是△ACD的外接圆⊙O的直径,CD交AB于点F,其中AC=AD,AD的延长线交过点B的切线BM于点E.
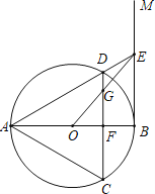
(1)求证:CD∥BM;
(2)连接OE交CD于点G,若DE=2,AB=4![]() ,求OG的长.
,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,点O是对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,下列结论:
①图形中全等的三角形只有三对; ②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF=OA;⑤AE2+BE2=2OPOB.其中正确的个数有( )个.
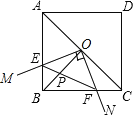
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com