
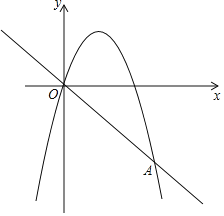
����Ŀ����ͼ����֪һ�κ���y����x����κ���y����x2+bx+c��ͼ���ཻ��ԭ��O����һ��A��4����4����
��1������κ�������ʽ��
��2��ֱ��x��m��x��m+2�ֱ��߶�AO��C��D�������κ���y����x2+bx+c��ͼ���ڵ�E��F����mΪ��ֵʱ���ı���CEFD��ƽ���ı��Σ�
��3���ڵڣ�2����������£���CE��x��Ľ���ΪM������COM�Ƶ�O��ʱ����ת�õ���C��OM�䣬��C�䡢M�䡢F�����һ�ι���ʱ���뻭��ͼ�β�ֱ��д����C��������꣮
���𰸡���1��y����x2+3x����2����mΪ1ʱ���ı���CEFD��ƽ���ı��Σ���3��ͼ���������C�䣨![]() ��
��![]() ����
����
��������
��1���ѣ�0��0����A��4����4������y��-x2+bx+c��������⣻
��2����C��m����m����D��m+2����m��2������ʾ��E��F���꣬����CE��DF���ɵõ�CE��DFʱ���ı���CEFDΪƽ���ı��Σ�����m2+3m+m����m2��m+2+m+2��������⣻
��3����C��H��x����H����֤��FHC���ס�FM��O����![]() ����
����![]() ��������⣮
��������⣮
�⣺��1���ѣ�0��0����A��4��-4������y����x2+bx+c��![]() ��
��
��ã�![]() ��
��
�������ߵı���ʽΪ��y����x2+3x��
��2����C��m����m����D��m+2����m��2����
��E��m����m2+3m����F[m+2������m+2��2+3��m+2��]����F��m+2����m2��m+2����
��CE��DF��
�൱CE��DFʱ���ı���CEFDΪƽ���ı��Σ�
����m2+3m+m����m2��m+2+m+2��
���m��1��
����mΪ1ʱ���ı���CEFD��ƽ���ı��Σ�
��3����ͼ���£���C��H��x����H��
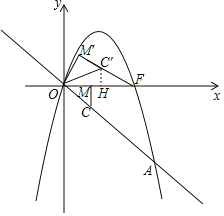
��m��1ʱ��C��1��-1����D��3��-3����F��3��0������F��Ϊ��������x���һ�����㣬
��OM��CM��1��OC��![]() ��
��
�ߡ�COM�Ƶ�O��ʱ����ת�õ���C��OM����
��OM����C��M����1����OM��C������OMC��90����
��Rt��OM��F��FM����![]() ��2
��2![]() ��
��
��FC����2![]() ��1��
��1��
�ߡ�C��FH��OFM����
���FHC���ס�FM��O��
��![]() ����
����![]() ��
��
��FH��![]() ��C��H��
��C��H��![]() ��
��
��OH��OF��FH��![]() ��
��
��C����![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
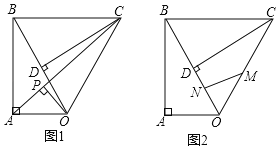
����Ŀ����֪Rt��OAB����OAB��90�㣬��ABO��30�㣬б��OB��4����Rt��OAB�Ƶ�O˳ʱ����ת60�㣬����BC
��1����ͼ1������AC����OP��AC������ΪP�����AOC��������߶�OP�ij���
��2����ͼ2����M���߶�OC���е㣬��N���߶�OB�ϵĶ��㣨�����O�غϣ������CMN�ܳ�����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
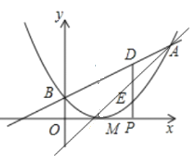
����Ŀ����֪���κ���ͼ��Ķ�������Ϊ![]() ��ֱ��
��ֱ��![]() ����κ�����ͼ����
����κ�����ͼ����![]() ��
��![]() ���㣬����
���㣬����![]() �������Ϊ
�������Ϊ![]() ��
��![]() ����
����![]() ���ϣ�
���ϣ�
��1����![]() ��ֵ��������κ����Ľ���ʽ��
��ֵ��������κ����Ľ���ʽ��
��2����![]() ������һ��
������һ��![]() ��ʹ
��ʹ![]() ���ܳ���С���������ʱ
���ܳ���С���������ʱ![]() �����ꣻ
�����ꣻ
��3����![]() ��
��![]() ���ϵ�һ�����㣬��
���ϵ�һ�����㣬��![]() ��
��![]() ��Ĵ��߷ֱ���ֱ��
��Ĵ��߷ֱ���ֱ��![]() �Ͷ��κ�����ͼ����
�Ͷ��κ�����ͼ����![]() ��
��![]() ���㣮��
���㣮��![]() ʱ�����߶�
ʱ�����߶�![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ˮƽ�����A����һ������������з��������������·����һ�������ߣ��ڵ��������ΪB��������ֱ��AB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ����ɸ��ǵ�Բ����Ͱ����ͼ����������Ͱ�ڣ���֪AB=4�ף�AC=3�ף�����������߶�OM=5�ף�Բ����Ͱ��ֱ��Ϊ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�������ֱ�ڷ�Բ����Ͱ���٣� ����ʱ�������������Ͱ��.
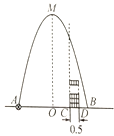
A.7B.8C.9D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ҵ��С����Ӧ������������ҵ���ĺ��٣���������С����Ϣ�������һ����Ʒ�꣮�õ깺��һ�ֽ��������е���Ʒ�������ۣ���Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�Ϊÿ��60Ԫʱ��ÿ�¿�����300�����г����鷴ӳ�������۸�ʱ���ۼ�ÿ��1Ԫÿ��Ҫ����10�����ۼ�ÿ�½�1Ԫÿ��Ҫ����20����Ϊ�˻�ø���������ֽ���Ʒ�ۼ۵���Ϊx��Ԫ/������ÿ����Ʒ����Ϊy��������������Ϊw��Ԫ����
��1��ֱ��д��y��x֮��ĺ�����ϵʽ��
��2�����ȷ���ۼ۲���ʹ��������������������
��3��Ϊ��ʹÿ����������6000ԪӦ��ο����ۼۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ϲ��������أ�ij�����̻����ο�����һ�ּӹ��õ������ϲˣ���֪ÿǧ�˳ɱ�Ϊ20Ԫ.�г����鷢�֣���һ��ʱ���ڣ��ò�Ʒ������![]() ��ǧ�ˣ������۵���
��ǧ�ˣ������۵���![]() ��Ԫ/ǧ�ˣ��ı仯���仯�����¹�ϵʽ��
��Ԫ/ǧ�ˣ��ı仯���仯�����¹�ϵʽ��![]() .�������ϲ������ʱ���ڵ���������Ϊ
.�������ϲ������ʱ���ڵ���������Ϊ![]() ��Ԫ��.
��Ԫ��.
��1����![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2�������ۼ۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3�������۲��Ź涨�þ��������ϲ˵����۵��۲��ø���28Ԫ/ǧ�ˣ����̻�ÿ���ܷ��ñ�150Ԫ��������������������������������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ���D��![]() �ϣ���E����AB�ϣ�E����A�غϣ������ı���BDCEΪ���Σ�
�ϣ���E����AB�ϣ�E����A�غϣ������ı���BDCEΪ���Σ�
��1����֤��AC=CE��
��2����֤��BC2��AC2=ABAC��
��3����֪��O�İ뾶Ϊ3��
����![]() =
=![]() ����BC�ij���
����BC�ij���
�ڵ�![]() Ϊ��ֵʱ��ABAC��ֵ���
Ϊ��ֵʱ��ABAC��ֵ���
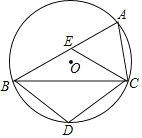
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У���A��B��C��D���ڱ߳�Ϊ1��С����������ĸ���ϣ�����M(1����2)��������y��mx2��2mx��n��m��0�����ܻ������� ��
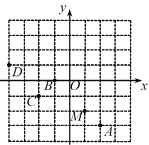
A.��AB.��BC.��CD.��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У������в�����ͼ��
���Ե�BΪԲ�ģ����ʵ���Ϊ�뾶��������AB�ڵ�M����BC�ڵ�N��
���ٷֱ��Ե�M�͵�NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�������������ڵ�G��
MN�ij�Ϊ�뾶�������������ڵ�G��
��������BG��AD��F��
�ܹ���A��AE��BF��BF�ڵ�P����BC�ڵ�E��
������EF��PD��
��1����֤���ı���ABEF�����Σ�
��2����AB��4��AD��6����ABC��60������DP�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com