
【题目】如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,

(1)若∠ABC=30°,∠ACB=50°,求∠DAE的度数
(2)写出∠DAE与∠C-∠B的数量关系,并证明你的结论
【答案】(1)10°;(2)∠DAE=![]() (∠C-∠B),证明见解析.
(∠C-∠B),证明见解析.
【解析】
(1)利用三角形内角和定理求得∠BAC=100°,根据角平分线定义可知∠EAC=![]() ∠BAC,再利用三角形内角和先求出∠DAC,再求得∠DAE;
∠BAC,再利用三角形内角和先求出∠DAC,再求得∠DAE;
(2)按照(1)中思路,进行推导即可解决问题.
(1)解:∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC=50°
∠BAC=50°
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=180°-90°-50°=40°
∴∠DAE=∠EAC-∠DAC=50°-40°=10°
(2)解:∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC=
∠BAC=![]() (180°-∠B-∠C)
(180°-∠B-∠C)
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=180°-90°-∠C=90°-∠C,
∴∠DAE=∠EAC-∠DAC=![]() (180°-∠B-∠C)-(90°-∠C)
(180°-∠B-∠C)-(90°-∠C)
=![]() (∠C-∠B)
(∠C-∠B)


科目:初中数学 来源: 题型:
【题目】(一)阅读
求x+6x+11的最小值.
解:x+6x+11
=x2+6x+9+2
=(x+3)2+2
由于(x+3)2的值必定为非负数,所以(x+3)2+2,即x2+6x+11的最小值为2.

(二)解决问题
(1)若m2+2mn+2n2-6n+9=0,求(![]() )-3的值;
)-3的值;
(2)对于多项式x2+y-2x+2y+5,当x,y取何值时有最小值,最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=-![]() 的图象的两个分支分布在第_________象限,在每个象限内,y随x的增大而_________,函数y=
的图象的两个分支分布在第_________象限,在每个象限内,y随x的增大而_________,函数y=![]() 的图象的两个分支分布在第_________象限,在每一个象限内,y随x的减小而_________.
的图象的两个分支分布在第_________象限,在每一个象限内,y随x的减小而_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 的外角平分线上一点,且满足
的外角平分线上一点,且满足![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )
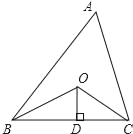
A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com