
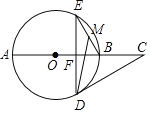
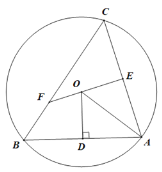
【题目】如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F,交⊙O于点E,点M是BE的中点,AB=4,∠E=∠C=30°.
(1)求证:CD是⊙O的切线;
(2)求DM的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由圆周角定理得出∠DOC=2∠E=60°,∠ODC=180°﹣(∠DOC+∠C)=90°,即可得出结论;
(2)连接OE、OM,证明∠DOC=∠COE=60°,由OB=OE,点M是BE的中点,得出∠BOM=![]() ∠COE=30°,OM⊥BE,则∠DOM=∠DOC+∠BOM=90°,OM=OBcos∠BOM=
∠COE=30°,OM⊥BE,则∠DOM=∠DOC+∠BOM=90°,OM=OBcos∠BOM=![]() ,由勾股定理得DM=
,由勾股定理得DM=![]() =
=![]() .
.
(1)证明:连接OD,如图1所示:
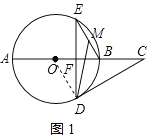
∵∠E=30°,
∴∠DOC=2∠E=60°,
∴∠DOC+∠C=60°+30°=90°,
∴∠ODC=180°﹣(∠DOC+∠C)=180°﹣90°=90°,即OD⊥CD,
∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)解:连接OE、OM,如图2所示:
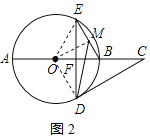
∵⊙O的直径AB,AB=4,
∴OB=OD=2,
∵OD=OE,DF⊥AB,
∴∠DOC=∠COE=60°,
∵OB=OE,点M是BE的中点,
∴∠BOM=![]() ∠COE=30°,OM⊥BE,
∠COE=30°,OM⊥BE,
∴∠DOM=∠DOC+∠BOM=60°+30°=90°,
∵在Rt△OMB中,∠OMB=90°,
∴OM=OBcos∠BOM=2cos30°=2×![]() =
=![]() ,
,
由勾股定理得:DM=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
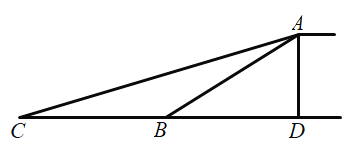
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,![]() ≈1.414,
≈1.414,![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯![]() 长为
长为![]() ,坡角
,坡角![]() 为
为![]() ”改造后的斜坡式自动扶梯的坡角
”改造后的斜坡式自动扶梯的坡角![]() 为
为![]() ,若国标规定自动扶梯的速度一般是
,若国标规定自动扶梯的速度一般是![]() ,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据:
,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形纸片![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,点B在x轴的正半轴上,点
,点B在x轴的正半轴上,点![]() 是边
是边![]() 上的一个动点(点P不与点O、B重合),过点P作
上的一个动点(点P不与点O、B重合),过点P作![]() 于点D,沿
于点D,沿![]() 折叠该纸片,使点O落在射线
折叠该纸片,使点O落在射线![]() 上的Q点处.
上的Q点处.
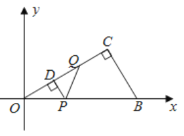
(Ⅰ)用含t的代数式表示线段![]() 的长;
的长;
(Ⅱ)当点Q与点C重合时,求t的值;
(Ⅲ)设![]() 与四边形
与四边形![]() 重叠部分的图形的面积为S,求S与t之间的函数关系式;
重叠部分的图形的面积为S,求S与t之间的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示放置,其中顶点 B1 在 y 轴上,顶点 C1,E1,E2,C2,E3,E4,C3… 在 x 轴上.已知正方形 A1B1C1D1 的边长为 1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则正方形 A2020B2020C2020D2020 的边长是______.
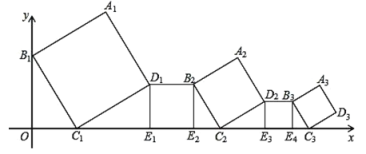
查看答案和解析>>
科目:初中数学 来源: 题型:
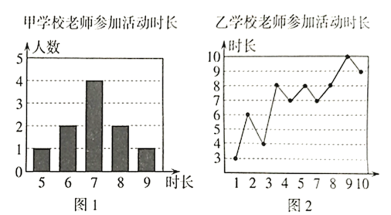
【题目】甲、乙两所学校选派相同人数的老师参加志愿者活动,參加活动时长分别被制成下列两个统计图,根据以上信息,整理分析数据如下表:
平均时间/小时 | 中位数/小时 | 众数/小时 | 方差/小时 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
![]() 求出表格中
求出表格中![]() 的值.
的值.
![]() 分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
查看答案和解析>>
科目:初中数学 来源: 题型:
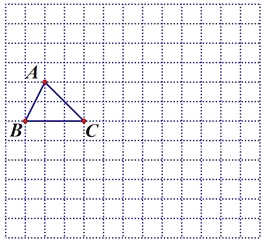
【题目】如图,在边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度后得到△A1B1C1.画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2.画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1(画图中要体现找关键点的方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在美化校园的活动中,数学兴趣小组用16m长的篱笆,一边靠墙围成一个矩形花园ABCD,墙长为6m,设AB![]() m.
m.
(1)若花园的面积为14![]() ,求
,求![]() 的值;
的值;
(2)花园的面积能否为40![]() ?为什么?
?为什么?
(3)若要求花园的面积大于24![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com