
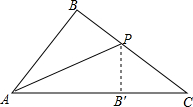
 如图,△ABC中,AB=6,BC=8,AC=10,把△ABC沿AP折叠,使边AB与AC重合,点B落在AC边上的B′处,则折痕AP的长等于3$\sqrt{5}$.
如图,△ABC中,AB=6,BC=8,AC=10,把△ABC沿AP折叠,使边AB与AC重合,点B落在AC边上的B′处,则折痕AP的长等于3$\sqrt{5}$. 分析 首先证明∠B=90°,设PB=PB′=x,在RT△PB′C中利用勾股定理求出x,再在RT△APB中利用勾股定理求出AP即可.
解答 解:∵AB=6,BC=8,AC=10,
∴AB2+BC2=AC2,
∴∠B=90°
∵△APB′是由 APB翻折,
APB翻折,
∴AB=AB′=6,PB=PB′,∠B=∠AB′P=∠PB′C=90°设PB=PB′=x,
在RT△PB′C中,∵B′C=AC-AB=4,PC=8-x,
∴x2+42=(8-x)2,
∴x=3,
∴AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
故答案为3$\sqrt{5}$.
点评 本题考查勾股定理的逆定理、勾股定理、翻折不变性等知识,证明∠B=90°是解题的关键,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
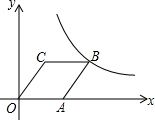 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | 2+$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
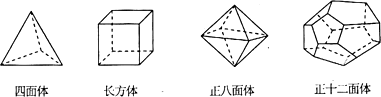
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同旁内角相等,两直线平行 | |
| B. | 等腰三角形的两个底角相等 | |
| C. | 同角(等角)的补角相等 | |
| D. | 三角形的一个外角大于任何一个与它不相邻的内角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
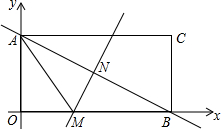 如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).
如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com