
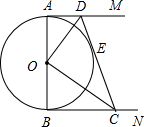 如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.
如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.分析 (1)根据切线长定理得到OD平分∠ADE,OC平分∠BCE,即∠ODC=∠ADC,∠OCD=∠BCD,再根据切线的性质AB⊥AM,AB⊥BN,则AM∥BN,利用平行线的性质得∠ADC+∠BCD=180°,所以∠ODC+∠OCD=90°,则根据三角形内角和可就是出∠DOC=90°;
(2)连接OE,如图,利用勾股定理可就是出CD=5,再根据切线长定理得到OE⊥DC,则利用面积法克就是出OE,从而得到AB的长.
解答 (1)证明:∵AM、BN是⊙O的切线,DE切⊙O于E,
∴OD平分∠ADE,OC平分∠BCE,
∴∠ODC=∠ADC,∠OCD=∠BCD,
∵AM、BN是⊙O的切线,
∴AB⊥AM,AB⊥BN,
∴AM∥BN,
∴∠ADC+∠BCD=180°,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°;
(2)解:连接OE,如图,在Rt△OCD中,∵OD=3,OC=4,
∴CD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵DE切⊙O于E,
∴OE⊥DC,
∵OE•CD=OD•OC,
∴OE=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴AB=2OE=$\frac{24}{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
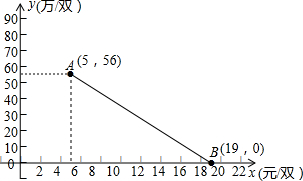 某袜业公司向上海世博会申请了在自己生产的袜子上印上海世博会会徽的专利权,但组委会只允许这种袜子在5月1日至5月31日这一个月内在全国各地生产销售.生产这种袜子的成本为每双5元,该袜业公司经过一段时间调查与分所后,发现这种袜子在5月份销售期间,每双袜子的销售单价x(元)和日均销售量y(万双)满足如图所示关系;日均各种费用等固定成本为20万元.
某袜业公司向上海世博会申请了在自己生产的袜子上印上海世博会会徽的专利权,但组委会只允许这种袜子在5月1日至5月31日这一个月内在全国各地生产销售.生产这种袜子的成本为每双5元,该袜业公司经过一段时间调查与分所后,发现这种袜子在5月份销售期间,每双袜子的销售单价x(元)和日均销售量y(万双)满足如图所示关系;日均各种费用等固定成本为20万元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
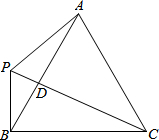 如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.
如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )| A. | $\frac{\sqrt{3}}{3}$,20m | B. | $\sqrt{3}$,10$\sqrt{3}$m | C. | 30°,20m | D. | 60°,10$\sqrt{3}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com