
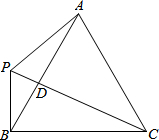
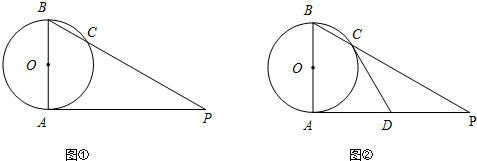
 如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.
如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.分析 (1)首先根据三角形的内角和求得∠PBC+∠PCB=120°,再根据等边三角形的内角为60°,得到∠PBA+∠PCB=60°,∠ACB=∠PCB+∠PCA=60°,即可得到∠PBA=∠PCA.
(2)如图,延长BP至E,使PE=PA,连接AE,证明△PAE为等边三角形,得到AE=AP=PE,∠PAE=60°,由△ABC为等边三角形,证明△AEB≌△APC(SAS),得到EB=PC,即可解答.
解答 解:(1)∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵∠BPC=60°,
∴∠PBC+∠PCB=180°-60°=120°,
∴∠PBA+∠ABC+∠PCB=120°,
∴∠PBA+∠PCB=60°,
∵∠ACB=∠PCB+∠PCA=60°,
∴∠PBA=∠PCA.
(2)如图,延长BP至E,使PE=PA,连接AE,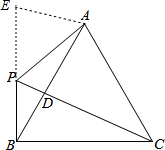
∵∠PBA=∠PCA,
∴点A,P,B,C四点共圆,
∴∠APC=∠ABC=60°,
∴∠APE=180°∠BPC-∠APC=60°,
又∵PE=PA,
∴△PAE为等边三角形,
∴AE=AP=PE,∠PAE=60°,
∵△ABC为等边三角形,
∴AC=BC,∠BCA=60°,
∴∠BAC=∠PAE,
∴∠BAC+∠PAD=∠PAE+∠PAD,
即:∠EAB=∠PAC,
在△AEB和△APC中,
$\left\{\begin{array}{l}{AE=AP}\\{∠EAB=∠PAC}\\{AB=AC}\end{array}\right.$,
∴△AEB≌△APC(SAS),
∴EB=PC,
∵BE=BP+PE=PB+PA,
∴PC=PB+PA.
点评 本题主要考查等边三角形的性质和判定,全等三角形的性质和判定,解决本题的关键是正确作出辅助线.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
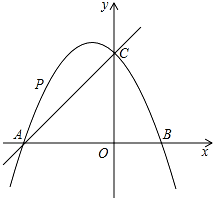 在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A、B,与y轴交于点C,直线y=x+4经过A、C两点,
在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A、B,与y轴交于点C,直线y=x+4经过A、C两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
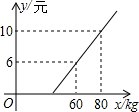 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
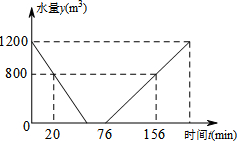 江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式
江阴水魔方游泳池常需进行换水清洗,途中的折线表示的是某个游泳池换水清洗过程“排水--清洗--灌水”中水量y(m3)与时间t(min)之间的函数关系式查看答案和解析>>
科目:初中数学 来源: 题型:解答题
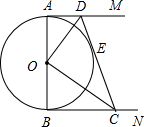 如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.
如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
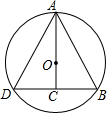 如图,Rt△ABC中,∠C=90°、∠BAC=30°,在AC边上取点O画圆使⊙O经过A、B两点,延长BC交⊙O于D;求证:A、B、D是⊙O的三等分点.
如图,Rt△ABC中,∠C=90°、∠BAC=30°,在AC边上取点O画圆使⊙O经过A、B两点,延长BC交⊙O于D;求证:A、B、D是⊙O的三等分点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com