
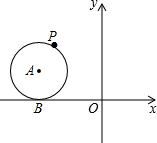
 如图,A点的坐标为(-2,1),以A为圆心的⊙A切x轴于点B,P(m,n)为⊙A上的一个动点,请探索n+m的最大值.
如图,A点的坐标为(-2,1),以A为圆心的⊙A切x轴于点B,P(m,n)为⊙A上的一个动点,请探索n+m的最大值. 分析 设m+n=k,则点P(m,n)在直线x+y=k上,易得直线y=-x+k与y轴的交点坐标为(0,k),于是可判断当直线y=-x+k与⊙A在上方相切时,k的值最大;直线y=-x+k与x轴交于点C,切⊙A于P,作PD⊥x轴于D,AE⊥PD于E,连接AB,如图,则C(k,0),利用直线y=-x+k的性质易得∠PCD=45°,则△PCD为等腰直角三角形,接着根据切线长定理和切线的性质得AB⊥OB,AP⊥PC,AP=AB=1,CP=CB=k+2,所以四边形ABDE为矩形,∠APE=45°,则DE=AB=1,PE=$\frac{\sqrt{2}}{2}$AP=$\frac{\sqrt{2}}{2}$,所以PD=PE+DE=$\frac{\sqrt{2}}{2}$+1,然后在Rt△PCD中,利用PC=$\sqrt{2}$PD得到2+k=$\sqrt{2}$($\frac{\sqrt{2}}{2}$+1),解得k=$\sqrt{2}$-1,从而得到n+m的最大值为$\sqrt{2}$-1.
解答 解:设m+n=k,则点P(m,n)在直线x+y=k上,当x=0时,y=k,即直线y=-x+k与y轴的交点坐标为(0,k),
所以当直线y=-x+k与⊙A在上方相切时,k的值最大,
直线y=-x+k与x轴交于点C,切⊙A于P,作PD⊥x轴于D,AE⊥PD于E,连接AB,如图,
当y=0时,-x+k=0,解得x=k,则C(k,0),
∵直线y=-x+k为直线y=-x向上平移k个单位得到,
∴∠PCD=45°,
∴△PCD为等腰直角三角形,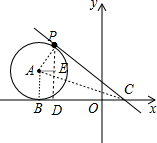
∵CP和OB为⊙A的切线,
∴AB⊥OB,AP⊥PC,AP=AB=1,CP=CB=k+2,
∴四边形ABDE为矩形,∠APE=45°,
∴DE=AB=1,
∵△APE为等腰直角三角形,
∴PE=$\frac{\sqrt{2}}{2}$AP=$\frac{\sqrt{2}}{2}$,
∴PD=PE+DE=$\frac{\sqrt{2}}{2}$+1,
在Rt△PCD中,∵PC=$\sqrt{2}$PD,
∴2+k=$\sqrt{2}$($\frac{\sqrt{2}}{2}$+1),解得k=$\sqrt{2}$-1,
∴n+m的最大值为$\sqrt{2}$-1.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决本题的关键是确定直线y=-x+k与⊙A相切时n+m的最大值.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
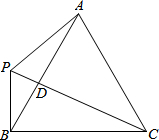 如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.
如图,△ABC为等边三角形,P是直线AB左侧一点,连接PA、PB、PC,PC与AB相交于点D,∠BPC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com