
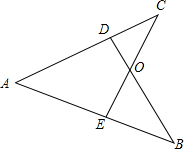
 如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC.
如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,且OD=OE,求证:AB=AC. 分析 根据垂直的定义得到∠CDO=∠BEO=90°,推出△CDO≌△BEO,根据全等三角形的性质得到∠C=∠B,OC=OB,证得CE=BD,推出△ABD≌△ACE,根据全等三角形的性质即可得到结论.
解答 证明:∵CE⊥AB于E,BD⊥AC于D,
∴∠CDO=∠BEO=90°,
在△CDO与△BEO中,$\left\{\begin{array}{l}{∠CDO=∠BEO}\\{OD=OE}\\{∠COD=∠BOE}\end{array}\right.$,
∴△CDO≌△BEO,
∴∠C=∠B,OC=OB,
∴OC+OE=OB+OD,
即CE=BD,
在△ABD与△ACE中,$\left\{\begin{array}{l}{∠A=∠A}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE,
∴AB=AC.
点评 本题考查了全等三角形的判定和性质,垂直的定义,熟练掌握全等三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
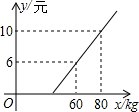 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票y(元)是行李质量x(kg)的一次函数,其图象如图.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
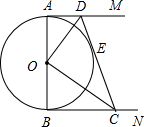 如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.
如图,AB是⊙O的直径,AM、BN是⊙O的切线,DE切⊙O于E,交AM于D,交BN于C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下,顶点坐标为(2,6) | B. | 开口向下,顶点坐标为(-2,6) | ||
| C. | 开口向上,顶点坐标为(-2,6) | D. | 开口向上,顶点坐标为(-2,-6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com