
【题目】世界上大部分国家都使用摄氏温度(℃),但美、英等国的天气预报仍然使用华氏温度(℉),两种计量之间有如下的对应表:
摄氏温度(℃) | 0 | 10 | 20 | 30 | 40 | 50 |
华氏温度(℉) | 32 | 50 | 68 | 86 | 104 | 122 |
由上表可以推断出,华氏0度对应的摄氏温度是_____℃,若某一温度时华氏温度的值与对应的摄氏温度的值相等,则此温度为_____℃.
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】为落实“促民生、促经济”政策,某市玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).下表是甲、乙两位职工今年四月份的工资情况信息:
职工 | 甲 | 乙 |
月销售件数/件 | 200 | 180 |
月工资/元 | 1800 | 1700 |
试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
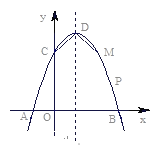
【题目】如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为![]() .
.
(1)求抛物线与![]() 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)求抛物线的解析式;
(3)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(4)若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1995年联合国教科文组织把每年4月23日确定为“世界读书日”.某中学为了解全校1000名学生平均每天阅读课外书报的时间,随机调查了该校50名学生一周内平均每天阅读课外书报的时间,结果如下表:
时间(分) | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
人 数 | 8 | 12 | 7 | 5 | 4 | 3 | 4 | 2 | 3 | 2 |
根据上述信息完成下列各题:
(1)在统计表(上表)中,众数是 分,中位数是 分;
(2)估计该学校平均每天阅读课外书报的时间不少于35分钟的学生大约 人;
小明同学根据上述信息制作了如下频数分布表和频数分布直方图,请你完成下列问题:
(3)频数分布表中![]() ,
,![]() ;
;
(4)补全频数分布直方图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的一条弦,点C是
的一条弦,点C是![]() 上一动点,且
上一动点,且![]() ,点E、F分别是AC、BC的中点,直线EF与
,点E、F分别是AC、BC的中点,直线EF与![]() 交于G、H两点.若
交于G、H两点.若![]() 的半径为5,则
的半径为5,则![]() 的最大值为______.
的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是半圆O中![]() 所对弦AB上一动点,过点P作PM⊥AB交
所对弦AB上一动点,过点P作PM⊥AB交![]() 于点M,作射线PN交
于点M,作射线PN交![]() 于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
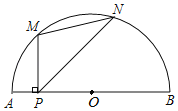
小超根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4.2 | 2.9 | 2.6 | 2.0 | 1.6 | 0 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当MN=2AP时,AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
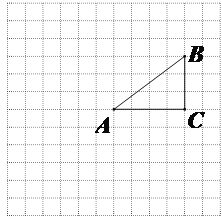
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(1,t+1),B(t-5,-1)两点.
的图象交于A(1,t+1),B(t-5,-1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=![]() 图象上任意两点,且满足c=n+1时,求
图象上任意两点,且满足c=n+1时,求![]() 的值.
的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<-3,0<x2<1,当x1x2=-3时,判断四边形NFEM的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com