
【题目】下图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120)。已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1) 当速度为50km/h、100km/h时,该汽车的耗油量分别为_____L/km、____L/km.
(2) 求线段AB所表示的y与x之间的函数表达式
(3) 速度是多少时,该汽车的耗油量最低?最低是多少?
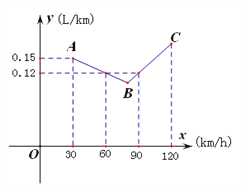
【答案】(1)0.13,0.14.(2)y=-0.001x+0.18;(3)速度是80 km/h 时,该汽车的耗油量最低,最低是0.1 L / km.
【解析】(1)和(2):先求线段AB的解析式,因为速度为50km/h的点 在AB上,所以将x=50代入计算即可,速度是100km/h的点在线段BC上,可由已知中的“该汽车的速度每增加1km/h,耗油量增加0,002L/km”列式求得,也可以利用解析式求解;
(3)观察图形发现,两线段的交点即为最低点,因此求两函数解析式组成的方程组的解即可.
解:(1)设AB的解析式为:y=kx+b,
把(30,0.15)和(60,0.12)代入y=kx+b中得:
![]() ,解得
,解得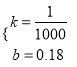 ,
,
∴AB:y=-0.001x+0.18,
当x=50时,y=-0.001×50+0.18=0.13,
由线段BC上一点坐标(90,0.12)得:0.12+(100-90)×0.002=0.14,
故答案为:0.13,0.14;
(2)设线段AB 所表示的y 与x 之间的函数表达式为y=kx+b.
因为y=kx+b 的图像过点(30,0.15)与(60,0.12),所以![]()
解方程组,得k=-0.001,b=0.18.
所以线段AB 所表示的y 与x 之间的函数表达式为y=-0.001x+0.18.
(3)根据题意,得线段BC 所表示的y 与x 之间的函数表达式为y=0.12+0.002(x-90)
=0.002x-0.06.
由图像可知,B 是折线ABC 的最低点.
解方程组![]() ,得
,得![]() .
.
因此,速度是80 km/h 时,该汽车的耗油量最低,最低是0.1 L / km.
“点睛”本题考查了一次函数的应用,正确求出两线段的解析式是解好本题的关键,因为系数为小数,计算要格外细心。容易出错,另外,此题中求最值的方法:两图象的交点,方程组的解;同时还有机地把函数和方程结合起来,是数学解题方法之一,应该熟练掌握.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】某校规定期中考试成绩的40%和期末考试成绩的60%的和作为学生成绩总成绩.该校李红同学期中数学考了85分,她希望自己学期总成绩不低于90分,则她在期末考试中数学至少应得多少分?设她在期末应考x分,可列不等式为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,过C作⊙O的切线交AB的延长线于E,AD⊥CE于D,连结AC.
(1)求证:AC平分∠BAD.
(2)若tan∠CAD=![]() ,AD=8,求⊙O直径AB的长.
,AD=8,求⊙O直径AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
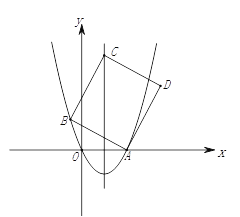
【题目】如图,抛物线![]() 交x轴的正半轴于点A,点B(
交x轴的正半轴于点A,点B(![]() ,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
(1)求a的值及点A的坐标;
(2)当点D恰好落在抛物线上时,求n的值;
(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n=___________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=![]() (c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围;
(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE和△ADC分别沿着边AB,AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( ) 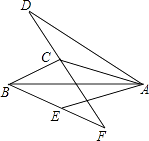
A.20°
B.30°
C.40°
D.45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com