
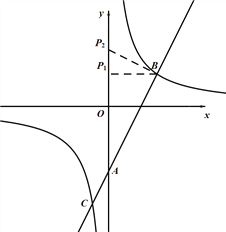
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=![]() (c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围;
(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.

【答案】(1)反比例函数解析式为: ![]() ,一次函数解析式为y1=2x﹣4;(2)由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3;(3)y轴上存在点P,使△PAB为直角三角形,P1(0,2)、P2(0,
,一次函数解析式为y1=2x﹣4;(2)由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3;(3)y轴上存在点P,使△PAB为直角三角形,P1(0,2)、P2(0, ![]() ).
).
【解析】试题分析:(1) 把B(3,2)代入![]() 求得k的值,即可得反比例函数解析式,把C(-1,n)代入反比例函数的解析式,求得n值,再利用待定系数法求一次函数的解析式即可;(2)观察图象,直接写出结论即可;(3)
求得k的值,即可得反比例函数解析式,把C(-1,n)代入反比例函数的解析式,求得n值,再利用待定系数法求一次函数的解析式即可;(2)观察图象,直接写出结论即可;(3)![]() 轴上存在点P,使△PAB为直角三角形,分∠B PA=90°和∠P BA=90°两种情况求点P的坐标即可.
轴上存在点P,使△PAB为直角三角形,分∠B PA=90°和∠P BA=90°两种情况求点P的坐标即可.
试题解析:
(1)把B(3,2)代入![]() 得:
得: ![]() =6
=6
∴反比例函数解析式为: ![]()
把C(-1,n)代入![]() ,得:n=-6
,得:n=-6
∴C(-1,-6)
把B(3,2)、C(-1,-6)分别代入![]() ,得:
,得:
![]() ,解得:
,解得: ![]()
所以一次函数解析式为![]()
(2)由图可知,当写出![]() >
>![]() 时
时![]() 的取值范围是-1<
的取值范围是-1<![]() <0或者
<0或者![]() >3
>3
(3)![]() 轴上存在点P,使△PAB为直角三角形
轴上存在点P,使△PAB为直角三角形
过B作BP1⊥![]() 轴于P1
轴于P1
∠B P1 A=90°,△P1AB为直角三角形
此时,P1(0,2)
过B作BP2⊥AB交![]() 轴于P2
轴于P2
∠P2 BA=90°,△P2 AB为直角三角形
在Rt△P1AB中,
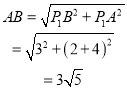
在Rt△P1 AB和Rt△P2 AB
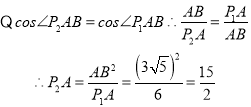
∴![]()
∴P2(0, ![]() )
)
综上所述,P1(0,2)、P2(0, ![]() )
)


科目:初中数学 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( ) 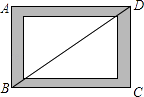
A.四边形ABCD由矩形变为平行四边形
B.BD的长度增大
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变
查看答案和解析>>
科目:初中数学 来源: 题型:
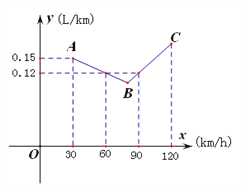
【题目】下图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120)。已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1) 当速度为50km/h、100km/h时,该汽车的耗油量分别为_____L/km、____L/km.
(2) 求线段AB所表示的y与x之间的函数表达式
(3) 速度是多少时,该汽车的耗油量最低?最低是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个菱形放在2倍的放大镜下,则下列说法中不正确的是 ( )
A. 菱形的边长扩大到原来的2倍B. 菱形的角的度数不变
C. 菱形的面积扩大到原来的2倍D. 菱形的面积扩大到原来的4倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:![]()
(1)已知点A,B,C表示的数分别为1,﹣ ![]() ,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M , N;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P , Q(用含m,n的式子表示这两个数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.
(1)问购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共100个,费用不超过8000元,问最多购买垃圾箱多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年,深圳市人居环境委通报了2014年深圳市大气PM2.5来源研究成果.报告显示主要来源有,A:机动车尾气,B:工业VOC转化及其他工业过程,C:扬尘,D:远洋船,E:电厂,F:其它.某教学学习小组根据这些数据绘制出了如下两幅尚不完整的统计图(图1,图2). 
请你根据统计图中所提供的信息解答下列问题:
(1)图2的扇形统计图中,x的值是;
(2)请补全图1中的条形统计图;
(3)图2的扇形统计图中,“A:机动车尾气”所在扇形的圆心角度数为度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读
(1)阅读理解: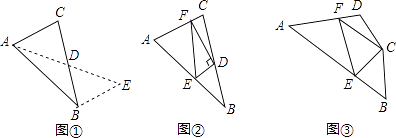
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com