
分析 根据分式的基本性质进行解答即可.
解答 解:分式$\frac{x+3}{{x}^{2}-9}$的分子分母同时除以x+3得,$\frac{x+3}{{x}^{2}-9}$=$\frac{1}{x-3}$;
分式$\frac{x+3}{x}$的分子分母同时乘以x-3得,$\frac{x+3}{x}$=$\frac{{x}^{2}-9}{x(x-3)}$;
分式$\frac{x}{3x-{x}^{2}}$的分子分母同时除以-x得,$\frac{x}{3x-{x}^{2}}$=$\frac{-1}{x-3}$.
故答案为:(x-3),x(x-3),-1.
点评 本题考查的是分式的基本性质,熟知分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
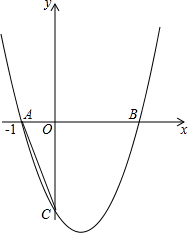 已知,如图,抛物线y=x2+bx+c的图象经过点A(-1,0),该抛物线与x轴的另一交点为B,与y轴的交点为C,tan∠CAO=3.
已知,如图,抛物线y=x2+bx+c的图象经过点A(-1,0),该抛物线与x轴的另一交点为B,与y轴的交点为C,tan∠CAO=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-1 | B. | x+1 | C. | $\frac{{x}^{2}+1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这跟芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这跟芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com