
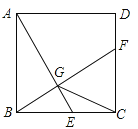
【题目】如图,已知正方形![]() 的边长为2,
的边长为2,![]() 是边
是边![]() 上的动点,
上的动点,![]() 交CD于F,垂足为G,连接
交CD于F,垂足为G,连接![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③点G运动的路径长为
;③点G运动的路径长为![]() ;④CG的最小值为
;④CG的最小值为![]() ;其中正确的是____________.
;其中正确的是____________.
【答案】②④
【解析】
根据正方形对角线的性质可得出当E移动到与C重合时,F点和D点重合,此时G点为AC中点,故①错误;求得∠BAE=∠CBF,根据正方形的性质可得AB=BC,∠ABC=∠C=90°,然后利用“角角边”证明△ABE和△BCF全等,根据全等三角形对应角相等可得AE=BF,判断出②正确;根据题意,G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,然后求出弧的长度,判断出③错误;由于OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,根据勾股定理求出最小CG长度.
解:∵在正方形ABCD中,BF⊥AE,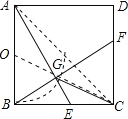
∴∠AGB保持90°不变,
∴G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,
∴当E移动到与C重合时,F点和D点重合,此时G点为AC中点,
∴AG=GE,故①错误;
∵BF⊥AE,
∴∠AEB+∠CBF=90°,
∵∠AEB+∠BAE=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中, ,
,
∴△ABE≌△BCF(AAS),
∴故②正确;
∵当E点运动到C点时停止,
∴点G运动的轨迹为![]() 圆,
圆,
圆弧的长=![]() π×2=
π×2=![]() ,故③错误;
,故③错误;
由于OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,
OC=![]() ,
,
CG的最小值为OC![]() OG=
OG=![]() ,故④正确;
,故④正确;
综上所述,正确的结论有②④.
故答案为:②④.


科目:初中数学 来源: 题型:
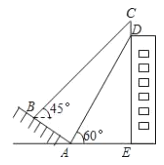
【题目】如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
A.15-5![]() B.20-10
B.20-10![]() C.10-5
C.10-5![]() D.5
D.5![]() -5
-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m.
(1)若移动滑块使AE=EF,求∠AFE的度数和棚宽BC的长.
(2)当∠AFE由60°变为74°时,问棚宽BC是增加还是减少?增加或减少了多少?(结果精确到0.1m.参考数据:![]() ≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
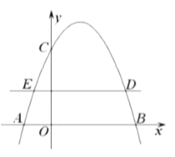
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() ,交抛物线于
,交抛物线于![]() 、
、![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)当![]() ,
,![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(3)当![]() 时,方程
时,方程![]() 在
在![]() 的范围内有实数解,请直接写出
的范围内有实数解,请直接写出![]() 的取值范围: .
的取值范围: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,图2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图1所示的位置时,求证:CD=AE.
(2)把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图2),分别连结DF、EF.
①找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
②试判断四边形CDFE的形状,并说明理由.
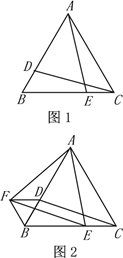
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
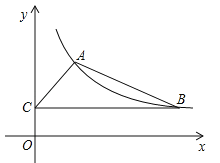
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离y(米)与小玲从家出发后步行的时间x(分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为_____米.
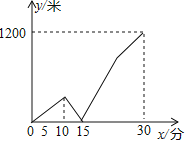
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
(Ⅰ)求点A,B和点C的坐标;
(Ⅱ)已知P是线段![]() 上的一个动点.
上的一个动点.
①若![]() 轴,交抛物线于点Q,当
轴,交抛物线于点Q,当![]() 取最大值时,求点P的坐标;
取最大值时,求点P的坐标;
②求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com