
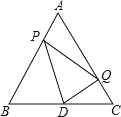
【题目】如图,△ABC是等边三角形,AB=2,D是边BC的中点,点P从点A出发,沿AB﹣BD以每秒1个单位长度的速度向终点D运动.同时点Q从点C出发,沿CA﹣AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动,设点P的运动时间为t(秒),△PQD的面积为S.
(1)求线段PB的长(用含t的代数式).
(2)当△PQD是等边三角形时,求t的值.
(3)当S>0时,求S与t的函数关系式.
(4)若点D关于直线PQ的对称点为点D′,且S>0,直接写出点D′落在△ABC的边上时t的值.
【答案】(1)BP=t﹣2;(2)1;(3)当0≤t≤2时,![]() ,当2<t<3时,
,当2<t<3时,![]() .(4)1或2.5.
.(4)1或2.5.
【解析】
试题分析: (1)根据当0≤t≤2和2≤t≤3时两种情况进行解答即可;
(2)根据等边三角形的性质和AAS证明△BPD与△CDQ全等解答即可;
(3)根据当0≤t≤2和2<t<3时两种情况,利用三角函数和三角形面积公式解答即可.
(4)根据点D′落在△ABC的边上两种情况解答即可.
试题解析:(1)∵△ABC是等边三角形,AB=2,
∴当0≤t≤2时,BP=2﹣t;
当2≤t≤3时,BP=t﹣2;
(2)如图1,∵△PQD是等边三角形,
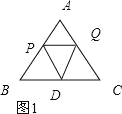
∴∠PDQ=60°,
∴∠PDB+∠CDQ=120°,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠PDB+∠BPD=120°,
∴∠BPD=∠CDQ,
∵BD=CD,
在△BPD与△CDQ中,
 ,
,
∴△BPD≌△CDQ(AAS),
∴BP=CQ,
∴2﹣t=t,
∴t=1,
(3)当0≤t≤2时,如图2,连接AD,

∵△ABC是等边三角形,D是边BC的中点,
∴∠ADB=90°,
∴AD=ABsin60°=![]() ,
,
分别过点P,Q作PE⊥BC,QF⊥BC,垂足分别为点E,F,
在Rt△BPE中,∠BEP=90°,PE=PBsin60°=![]() ,
,
在Rt△QCF中,∠QFC=90°,QF=CQsin60°=![]() ,
,
过点Q作QG⊥AB于点G,
在Rt△AGQ中,∠AGQ=90°,QG=AQsin60°=![]() ,
,
∴S△PQD=S△ABC﹣S△BPD﹣S△QCD﹣S△APQ,
∴![]() ,
,
∴![]() ,
,
当2<t<3时,如图3

过点Q作QH⊥BC于点H,
在Rt△CQH中,∠CHQ=90°,
QH=CQsin60°=![]() ,
,
∴![]() ,
,
∴![]() .
.
(4)点D′落在△ABC的边上,如图4,此时t=1;

点D′落在△ABC的边上,如图5,此时t=2.5.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲乙两人玩一个游戏,判定这个游戏公平不公平的标准是( )
A. 游戏的规则由甲方确定
B. 游戏的规则由乙方确定
C. 游戏的规则由甲乙双方商定
D. 游戏双方要各有50%赢的机会
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若圆的半径是5, 如果点P到圆心的距离为4.5,那么点P与⊙O的位置关系是( )
A. 点P在⊙O外 B. 点P在⊙O内
C. 点P在⊙O上 D. 点P在⊙O外或⊙O上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形,属于因式分解的是( )
A. a(x﹣y)=ax﹣ayB. x2+3x+2=x(x+3)+2
C. (x+y)(x﹣y)=x2﹣y2D. x3﹣x=x(x+1)(x﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
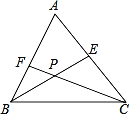
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.
(1)若∠ABC=70°,∠ACB=50°,则∠BPC= °;
(2)求证:∠BPC=180°﹣![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com