
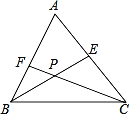
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.
(1)若∠ABC=70°,∠ACB=50°,则∠BPC= °;
(2)求证:∠BPC=180°﹣![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.
【答案】(1)120°;(2)证明见解析;(3)∠BPC=90°+![]()
![]() .
.
【解析】试题分析:(1)根据已知条件求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解;(2)根据三角形的内角和和角平分线的定义即可得到结论;(3)根据三角形的内角和和角平分线的定义即可得到结论.
试题解析:(1)PBC+∠PCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() ×120°=60°,
×120°=60°,
在△PBC中,∠BPC=180°(∠PBC+∠PCB)=180°60°=120°
故答案为:120;
(2)证明:∵∠ABC和∠ACB的平分线BE、CF相交于点P,
∴∠PBC=![]() ∠ABC, ∠PCB=
∠ABC, ∠PCB=![]() ∠ACB,
∠ACB,
∵∠BPC +∠PBC+∠PCB=180°,
∴∠BPC=180°-(∠PBC+∠PCB)= 180°-(![]() ∠ABC +
∠ABC +![]() ∠ACB) =180°-
∠ACB) =180°-![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠BPC=180°-![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∵由(2)可知:∠BPC=180°-![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠BPC=180°-![]() (180°-∠A),
(180°-∠A),
∵∠A= ![]() ,
,
∴∠BPC=180°-![]() (180°-
(180°- ![]() )=90°+
)=90°+![]()
![]() .
.


科目:初中数学 来源: 题型:
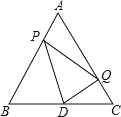
【题目】如图,△ABC是等边三角形,AB=2,D是边BC的中点,点P从点A出发,沿AB﹣BD以每秒1个单位长度的速度向终点D运动.同时点Q从点C出发,沿CA﹣AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动,设点P的运动时间为t(秒),△PQD的面积为S.
(1)求线段PB的长(用含t的代数式).
(2)当△PQD是等边三角形时,求t的值.
(3)当S>0时,求S与t的函数关系式.
(4)若点D关于直线PQ的对称点为点D′,且S>0,直接写出点D′落在△ABC的边上时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
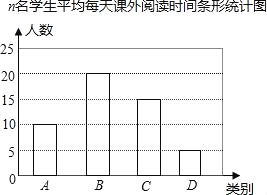
【题目】课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.
(1)求n的值.
(2)四类中人数最多的是 (用A、B、C、D作答),选择该类的学生人数占被调查的学生人数的百分比为 .
(3)该校现有1300名学生,估计该校学生课外阅读时间不少于1小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次函数y=x2-4x+1化成y=a(x-h)2+k的形式是( )
A. y=(x-2)2+1 B. y=(x-2)2-1 C. y=(x-2)2-3 D. y=(x-2)2+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com