
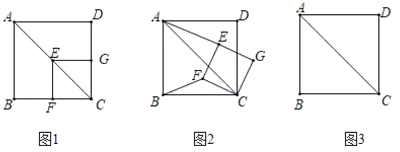
【题目】如图1,边长为4的正方形与边长为![]() 的正方形
的正方形![]() 的顶点
的顶点![]() 重合,点
重合,点![]() 在对角线
在对角线![]() 上.
上.
问题发现
(1)如图1,![]() 与
与![]() 的数量关系为______.
的数量关系为______.
类比探究
(2)如图2,将正方形![]() 绕点
绕点![]() 旋转
旋转![]() 度(
度(![]() ).请问(1)中的结论还成立吗?若不成立,请说明理由.
).请问(1)中的结论还成立吗?若不成立,请说明理由.
拓展延伸
(3)若![]() 为
为![]() 的中点,在正方形
的中点,在正方形![]() 的旋转过程中,当点
的旋转过程中,当点![]() ,
,![]() ,
,![]() 在一条直线上时,线段
在一条直线上时,线段![]() 的长度为______.
的长度为______.
【答案】(1)![]() ;(2)成立,见解析;(3)
;(2)成立,见解析;(3)![]() 或
或![]()
【解析】
问题发现:证出AB∥EF,由平行线分线段成比例定理得出![]() ,即可得出结论;
,即可得出结论;
类比探究:证明△ACE∽△BCF,得出![]() ,即可的结论;
,即可的结论;
拓展延伸:分两种情况,连接CE交GF于H,由正方形的性质得出AB=BC=4,![]() ,
,![]() ,GH=HF=HE=HC,得出
,GH=HF=HE=HC,得出![]() ,
,![]() ,
,![]() ,由勾股定理求出
,由勾股定理求出![]() ,即可得出答案.
,即可得出答案.
[问题发现]
解:![]() ,理由如下:
,理由如下:
∵四边形ABCD和四边形CFEG是正方形,
∴∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE=![]() CF,CE⊥GF,
CF,CE⊥GF,
∴AB∥EF,
∴![]() ,
,
![]() ;
;
故答案为:![]() ;
;
[类比探究]
解:上述结论还成立,理由如下:
连接CE,如图2所示:
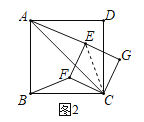
∵∠FCE=∠BCA=45°,
∴∠BCF=∠ACE=45°-∠ACF,
在Rt△CEG和Rt△CBA中,
![]() ,
,
![]() ,
,
∴△ACE∽△BCF,
![]() ,
,
![]() ;
;
[拓展延伸]
解:分两种情况:
①如图3所示:
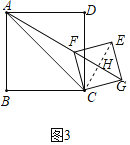
连接CE交GF于H,
∵四边形ABCD和四边形CFEG是正方形,
∴AB=BC=4,AC=![]() AB=4
AB=4![]() ,GF=CE=
,GF=CE=![]() CF,HF=HE=HC,
CF,HF=HE=HC,
∵点F为BC的中点,
∴CF=![]() BC=2,GF=CE=2
BC=2,GF=CE=2![]() ,GH=HF=HE=HC=
,GH=HF=HE=HC=![]() ,
,
∴![]() ,
,
∴![]() ;
;
②如图4所示:连接CE交GF于H,
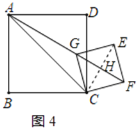
同①得:GH=HF=HE=HC=![]() ,
,
∴![]() ,
,
∴![]() ;
;
故答案为:![]() 或
或![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
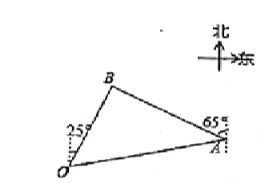
【题目】中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(![]() 点)尾(
点)尾(![]() 点)前去拦截,8分钟后同时到达
点)前去拦截,8分钟后同时到达![]() 点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东
点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东![]() ,乙直升机的航向为北偏西
,乙直升机的航向为北偏西![]() ,求乙直升机的飞行速度(单位:海里/小时).
,求乙直升机的飞行速度(单位:海里/小时).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与函数y=![]() (x>0)的图象交于点A(1,2).
(x>0)的图象交于点A(1,2).
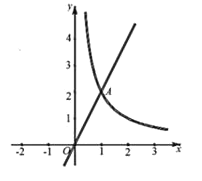
(1)求m的值;
(2)过点A作x轴的平行线l,直线y=2x+b与直线l交于点B,与函数y=![]() (x>0)的图象交于点C,与x轴交于点D.
(x>0)的图象交于点C,与x轴交于点D.
①若点C是线段BD的中点时,则点C的坐标是________,b的值是________;
②当BC>BD时,直接写出b的取值范围________.
查看答案和解析>>
科目:初中数学 来源: 题型:
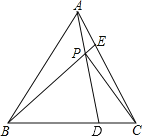
【题目】如图,在边长为![]() 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() 是
是![]() 的中点,以点
的中点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() 、
、![]() 始终与矩形
始终与矩形![]() 、
、![]() 两边相交,
两边相交,![]() ,
,![]() ,
,
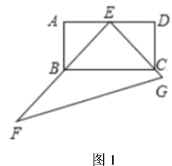
(1)如图1,当![]() 、
、![]() 分别过点
分别过点![]() 、
、![]() 时,求
时,求![]() 的大小;
的大小;
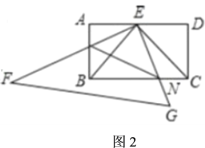
(2)在(1)的条件下,如图2,将![]() 绕点按顺时针方向旋转,当旋转到
绕点按顺时针方向旋转,当旋转到![]() 与
与![]() 重合时停止转动.若
重合时停止转动.若![]() 、
、![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .
.
①在![]() 旋转过程中,四边形
旋转过程中,四边形![]() 的面积是否发生变化?若不变,求四边形
的面积是否发生变化?若不变,求四边形![]() 的面积;若要变,请说明理由.
的面积;若要变,请说明理由.
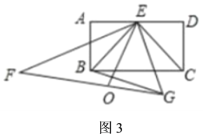
②如图3,设点![]() 为
为![]() 的中点,连结
的中点,连结![]() 、
、![]() ,若
,若![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018西安国际马拉松”于2018年10月20日在陕西西安举行,该赛事共有三项:![]() .“马拉松”、
.“马拉松”、![]() .“半程马拉松”、
.“半程马拉松”、![]() .“迷你马拉松”小明和小刚有幸参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
.“迷你马拉松”小明和小刚有幸参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为________.
(2)利用列表或树状图求小明和小刚被分配到不同项目组的概率________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com