
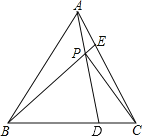
【题目】如图,在边长为![]() 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
A.1B.2C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:

请回答下列问题:
(1)求该校一共有班级________个;在扇形统计图中,贫困家庭学生人数有5名的班级所对应扇形圆心角为________°;
(2)将条形图补充完整;
(3)甲、乙、丙是贫困生中的三名学生,学校决定从这三名学生中随机抽取两名代表到市里进行发言,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
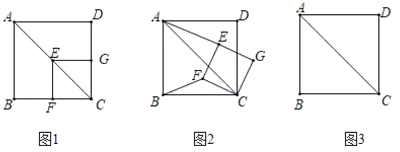
【题目】如图1,边长为4的正方形与边长为![]() 的正方形
的正方形![]() 的顶点
的顶点![]() 重合,点
重合,点![]() 在对角线
在对角线![]() 上.
上.
问题发现
(1)如图1,![]() 与
与![]() 的数量关系为______.
的数量关系为______.
类比探究
(2)如图2,将正方形![]() 绕点
绕点![]() 旋转
旋转![]() 度(
度(![]() ).请问(1)中的结论还成立吗?若不成立,请说明理由.
).请问(1)中的结论还成立吗?若不成立,请说明理由.
拓展延伸
(3)若![]() 为
为![]() 的中点,在正方形
的中点,在正方形![]() 的旋转过程中,当点
的旋转过程中,当点![]() ,
,![]() ,
,![]() 在一条直线上时,线段
在一条直线上时,线段![]() 的长度为______.
的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
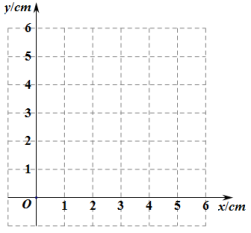
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海鲜门市的某种海鲜食材,成本为10元/千克,每天的进货量p(千克)与销售价格x(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
销售价格x(元/千克) | 10 | 12 | … | 30 |
市场需求量q(千克) | 30 | 28 | … | 10 |
(已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克)
(1)请写出q与x的函数关系式:___________________________;
(2)当每天的进货量小于或等于市场需求量时,这种海鲜食材能全部售出,而当每天的进货量大于市场需求量时,只能售出符合市场需求量的海鲜食材,剩余的海鲜食材由于保质期短而只能废弃.
①求出每天获得的利润y(元)与销售价格x的函数关系式;
②为了避免浪费,每天要确保这种海鲜食材能全部售出,求销售价格为多少元时,每天获得的利润(元)最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:

(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
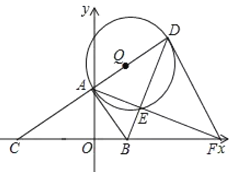
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,点B是
,点B是![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,过点A作
,过点A作![]() ,交
,交![]() 轴于点C,点D是点C关于点A的对称点,连接
轴于点C,点D是点C关于点A的对称点,连接![]() ,以
,以![]() 为直径作
为直径作![]() 交
交![]() 于点E,连接AE并延长交
于点E,连接AE并延长交![]() 轴于点F,连接DF.
轴于点F,连接DF.
(1)求线段AE的长;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 与
与![]() 相似,求
相似,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
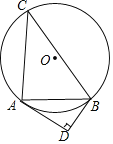
【题目】如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.
(1)求证:∠BAD+∠C=90°
(2)求线段AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com