
【题目】海鲜门市的某种海鲜食材,成本为10元/千克,每天的进货量p(千克)与销售价格x(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
销售价格x(元/千克) | 10 | 12 | … | 30 |
市场需求量q(千克) | 30 | 28 | … | 10 |
(已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克)
(1)请写出q与x的函数关系式:___________________________;
(2)当每天的进货量小于或等于市场需求量时,这种海鲜食材能全部售出,而当每天的进货量大于市场需求量时,只能售出符合市场需求量的海鲜食材,剩余的海鲜食材由于保质期短而只能废弃.
①求出每天获得的利润y(元)与销售价格x的函数关系式;
②为了避免浪费,每天要确保这种海鲜食材能全部售出,求销售价格为多少元时,每天获得的利润(元)最大值是多少?
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
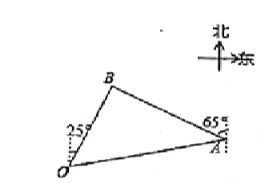
【题目】中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(![]() 点)尾(
点)尾(![]() 点)前去拦截,8分钟后同时到达
点)前去拦截,8分钟后同时到达![]() 点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东
点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东![]() ,乙直升机的航向为北偏西
,乙直升机的航向为北偏西![]() ,求乙直升机的飞行速度(单位:海里/小时).
,求乙直升机的飞行速度(单位:海里/小时).
查看答案和解析>>
科目:初中数学 来源: 题型:
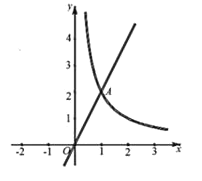
【题目】如图,直线y=2x与函数y=![]() (x>0)的图象交于点A(1,2).
(x>0)的图象交于点A(1,2).
(1)求m的值;
(2)过点A作x轴的平行线l,直线y=2x+b与直线l交于点B,与函数y=![]() (x>0)的图象交于点C,与x轴交于点D.
(x>0)的图象交于点C,与x轴交于点D.
①若点C是线段BD的中点时,则点C的坐标是________,b的值是________;
②当BC>BD时,直接写出b的取值范围________.
查看答案和解析>>
科目:初中数学 来源: 题型:
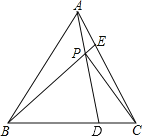
【题目】如图,在边长为![]() 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,顶点
轴上,顶点![]() 在第二象限,点
在第二象限,点![]() 的坐标为
的坐标为![]() .将线段
.将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至线段
至线段![]() ,若反比例函数y=
,若反比例函数y=![]() (k≠0)的图象经过A、D两点,则k值为_________.
(k≠0)的图象经过A、D两点,则k值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() 是
是![]() 的中点,以点
的中点,以点![]() 为直角顶点的直角三角形
为直角顶点的直角三角形![]() 的两边
的两边![]() 、
、![]() 始终与矩形
始终与矩形![]() 、
、![]() 两边相交,
两边相交,![]() ,
,![]() ,
,
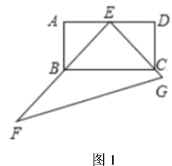
(1)如图1,当![]() 、
、![]() 分别过点
分别过点![]() 、
、![]() 时,求
时,求![]() 的大小;
的大小;
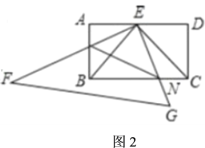
(2)在(1)的条件下,如图2,将![]() 绕点按顺时针方向旋转,当旋转到
绕点按顺时针方向旋转,当旋转到![]() 与
与![]() 重合时停止转动.若
重合时停止转动.若![]() 、
、![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .
.
①在![]() 旋转过程中,四边形
旋转过程中,四边形![]() 的面积是否发生变化?若不变,求四边形
的面积是否发生变化?若不变,求四边形![]() 的面积;若要变,请说明理由.
的面积;若要变,请说明理由.
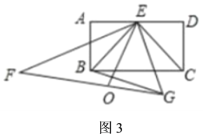
②如图3,设点![]() 为
为![]() 的中点,连结
的中点,连结![]() 、
、![]() ,若
,若![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m.
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年植树节,某中学组织师生开展植树造林活动,为了解全校800名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图.
(1)求![]() 的值,并将条形统计图补充完整;
的值,并将条形统计图补充完整;
(2)求从50名学生中任意抽取一名,植树数量恰好等于中位数的概率;
(3)估计该校800名学生中,植树数量不少于4棵的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com