
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)按照变量的定义,根据题意点P为动点,BE的长随着点P的移动而改变,BC为已知等腰直角三角形![]() 的斜边;
的斜边;
(2)描点画出图象即可;
(3)根据图形可求出![]() 长度根据
长度根据![]() 长度变化的函数关系式为一次函数,发现斜率绝对值接近
长度变化的函数关系式为一次函数,发现斜率绝对值接近![]() ,再通过画图可证明三条线段关系.
,再通过画图可证明三条线段关系.
(1)根据题意,画出图形,再结合表格数据可知,![]() 的长度是自变量,
的长度是自变量,![]() 的长度是这个自变量的函数,
的长度是这个自变量的函数,![]() 的长度是常量.
的长度是常量.
故答案为:![]() ,
,![]() ,
,![]() .
.
(2)根据表格数据描点画出以下图像
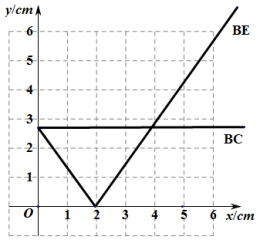
(3)首先通过函数图像图像,可判断BE关于BP的函数图像氛围两部分,斜率接近![]() ,则可知线段
,则可知线段![]() ,
,![]() ,
,![]() 之间的数量关系
之间的数量关系![]() .
.
再通过画图证明:
当点P在线段BA的延长线上时,如图,过点P作PF垂直于AC交BC的延长线于F,
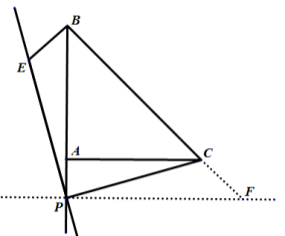
∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() (
(![]() ),
),
∴![]() ,
,
在等腰直角三角形![]() 中,
中,![]()
∴![]() ,
,
即,![]() ;
;
当点P在线段AB上时,过点P作![]() 于点
于点![]() ,
,
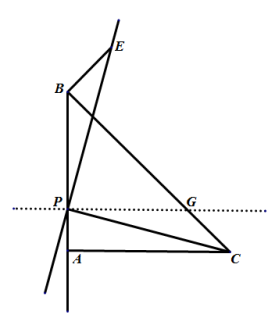
同理可证![]() (
(![]() ),
),
∴![]() ,
,
∴![]() ,
,
又∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]()
综上:线段![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 与
与![]() 的平分线,
的平分线,![]() 的延长线与
的延长线与![]() 相交于点
相交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
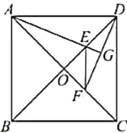
A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次学科测验,学生得分均为整数,满分为10分,成绩达到6分以上(包括6
分)为合格,成绩达到9分为优秀.这次测验甲、乙两组学生成绩分布的条形统计图如下:
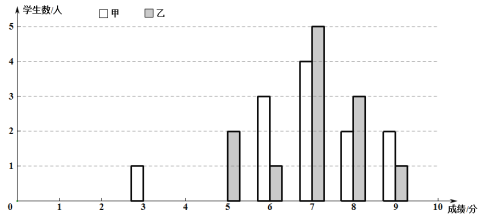
(1)请补充完成下面的成绩统计分析表:

(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组.请你给出三条支持乙组学生观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
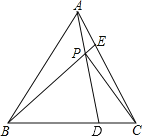
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在四边形ABCD中,AD∥BC, AB⊥BC,∠DCB=75,以CD为一边的等边△DCE的另一顶点E在边AB上.
(1)求∠AED的度数;
(2)连接AC,如图2所示,试判断△ABC的形状;
(3)如图3所示,若F为线段CD上一点,AB=4,∠FBC=30,求DF的长.
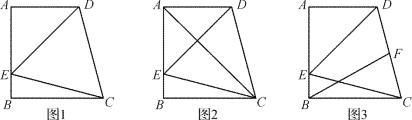
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
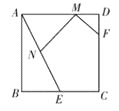
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com