
【题目】如图,已知在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 与
与![]() 的平分线,
的平分线,![]() 的延长线与
的延长线与![]() 相交于点
相交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
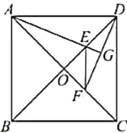
A.①②B.③④C.①②③D.①②③④
【答案】C
【解析】
由正方形的性质可得∠ACD=∠ADB=45°,根据三角形外角性质及角平分线的定义可得∠AFD=∠ADF,可证明AF=AD,根据等腰三角形“三线合一”的性质可得AG⊥DF,可得AG为DF的垂直平分线,可判定①正确;根据垂直平分线的性质可得EF=ED,可得∠EFD=∠EDF,即可证明∠EFD=∠FDC,可得EF//CD,即可证明EF//AB,可判定②正确;根据正方形的性质可得AB=AD,即可证明AB=AF,可判定③正确,由EF=ED,EF为Rt△EOF的斜边,可得ED>OE,即可得出EF不是△OCD的中位线,可得CD≠2EF,根据AB=CD即可判定④错误;综上即可得答案.
∵在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,
∴∠ACD=∠ADB=45°,∠DOC=90°,AB=AD,
∵DF为∠ODC的平分线,
∴∠ODF=∠CDF,
∴∠ADB+∠ODF=∠ACD+∠CDF,即∠AFD=∠ADF,
∴AD=AF,
∵AG为∠OAD的平分线,
∴AG⊥DF,故①正确,
∴AG为DF的垂直平分线,
∴ED=EF,
∴∠EFD=∠EDF,
∴∠EFD=∠CDF,
∴EF//CD,
∵AB//CD,
∴EF//AB,故②正确,
∵AD=AB,AD=AF,
∴AB=AF,故③正确,
∵EF=ED,EF为Rt△EOF的斜边,
∴ED>OE,
∵EF//CD,
∴EF不是△OCD的中位线,
∴CD≠2EF,即AB≠2EF,故④错误,
综上所述:正确的结论有①②③,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:![]() ≈1.732)
≈1.732)
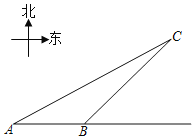
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲是小明设计的花边图案作品该作品由形如图乙的矩形图案拼接而成(不重叠,无缝隙).该矩形图案既是轴对称图形,又是中心对称图形.图乙中,![]() ,上、下两个半圆的面积之和为
,上、下两个半圆的面积之和为![]() ,中间阴影菱形的一组对边与
,中间阴影菱形的一组对边与![]() 平行,且菱形的面积比
平行,且菱形的面积比![]() 个角上的阴影三角形的面积之和大
个角上的阴影三角形的面积之和大![]() ,则
,则![]() 的长度为__________
的长度为__________![]()
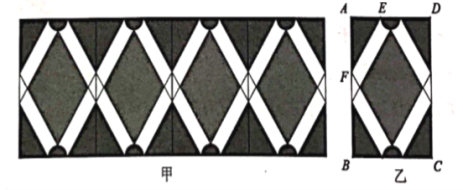
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:

请回答下列问题:
(1)求该校一共有班级________个;在扇形统计图中,贫困家庭学生人数有5名的班级所对应扇形圆心角为________°;
(2)将条形图补充完整;
(3)甲、乙、丙是贫困生中的三名学生,学校决定从这三名学生中随机抽取两名代表到市里进行发言,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() .
.
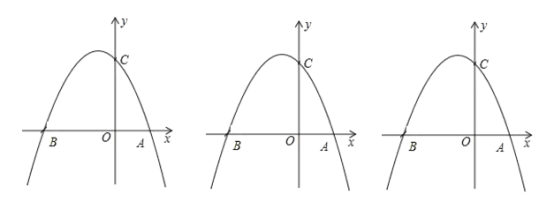
(1)求抛物线的解析式;
(2)点![]() 为第二象限抛物线上一点,连接
为第二象限抛物线上一点,连接![]() 、
、![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 做
做![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,过点
,过点![]() 做直线
做直线![]() 轴,在
轴,在![]() 轴上方直线
轴上方直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)在(2)的条件下,点![]() 为第二象限抛物线上的一点,连接
为第二象限抛物线上的一点,连接![]() ,过点
,过点![]() 做
做![]() 于点
于点![]() ,连接
,连接![]() ,线段
,线段![]() 、
、![]() 分别交线段
分别交线段![]() 于点
于点![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
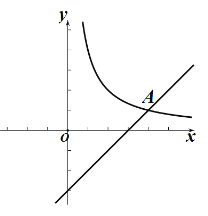
【题目】如图,在平面直角坐标系xOy中,函数![]() (k>0)的图象与直线y=x-3相交与点A(4,m).
(k>0)的图象与直线y=x-3相交与点A(4,m).
(1)求k、m的值;
(2)已知点P(a,a)(a>0),过点P作垂直于y轴的直线,交直线y=x-3于点M,过点P作垂直于x轴的直线,交函数![]() (k>0)的图象于点N.
(k>0)的图象于点N.
①当a=1时,判断PM与PN之间的数量关系,并说明理由;
②若PM≥PN,请结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com