
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() .
.
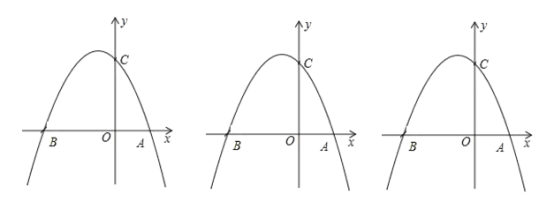
(1)求抛物线的解析式;
(2)点![]() 为第二象限抛物线上一点,连接
为第二象限抛物线上一点,连接![]() 、
、![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 做
做![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,过点
,过点![]() 做直线
做直线![]() 轴,在
轴,在![]() 轴上方直线
轴上方直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)在(2)的条件下,点![]() 为第二象限抛物线上的一点,连接
为第二象限抛物线上的一点,连接![]() ,过点
,过点![]() 做
做![]() 于点
于点![]() ,连接
,连接![]() ,线段
,线段![]() 、
、![]() 分别交线段
分别交线段![]() 于点
于点![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的长度.
的长度.
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3)![]()
【解析】
(1)令![]() ,求出y的值,即可求出C点坐标,根据
,求出y的值,即可求出C点坐标,根据![]() ,可求出B点坐标,把A、B点坐标代入解析式,即可求a、b的值,从而求出解析式;
,可求出B点坐标,把A、B点坐标代入解析式,即可求a、b的值,从而求出解析式;
(2)设![]() ,表示出
,表示出![]() ,
,![]() ,从而求出
,从而求出![]() ,从而推出
,从而推出![]() ,通过
,通过![]() ,列出关于m的方程,解方程求出m的值,即可求出PD的长;
,列出关于m的方程,解方程求出m的值,即可求出PD的长;
(3)过![]() 做
做![]() 交
交![]() 轴于
轴于![]() ,延长
,延长![]() 交
交![]() 延长线于
延长线于![]() ,过
,过![]() 做
做![]() ,连接
,连接![]() 并连延长交
并连延长交![]() 轴于
轴于![]() .证明
.证明![]() ,
,![]() ,通过相似三角形的性质可求出
,通过相似三角形的性质可求出![]() ,从而推出
,从而推出![]() ,设
,设![]() ,通过
,通过![]() ,可求出n的值,即可求出
,可求出n的值,即可求出![]() ,即可求出
,即可求出![]() 解析式为
解析式为![]() ,将
,将![]() 与抛物线解析式联立,解出x的值,从而求出Q的坐标,利用勾股定理可求
与抛物线解析式联立,解出x的值,从而求出Q的坐标,利用勾股定理可求![]() .
.
(1)![]() 对于
对于![]() 令
令![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
∴![]() ,
,
![]()
将![]() 、
、![]() 代入
代入![]()
∴![]() ,解得
,解得![]()
∴抛物线的解析式为![]()
(2)如图;
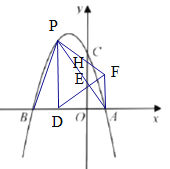
设![]()
![]() 轴
轴
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴![]()
∴![]()
![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]()
∴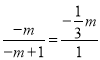
∴![]() ,
,
∴![]() ,
,
∴![]()
(3)过![]() 做
做![]() 交
交![]() 轴于
轴于![]() ,延长
,延长![]() 交
交![]() 延长线于
延长线于![]() ,过
,过![]() 做
做![]() ,连接
,连接![]() 并连延长交
并连延长交![]() 轴于
轴于![]() ,过Q点 作QP1⊥PC,交PC于点P1.
,过Q点 作QP1⊥PC,交PC于点P1.
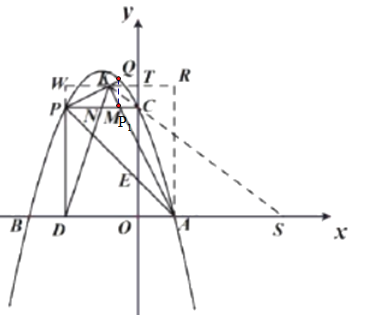
![]() ,
,
又![]() ,
,
![]()
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
设![]()
![]()
![]()
![]()
![]()
解得,![]() ,
,![]() (舍)
(舍)
![]() ,
,
∴![]() 解析式为
解析式为![]()
将![]() 与抛物线解析式联立
与抛物线解析式联立
![]()
解得,![]() (与
(与![]() 点重合舍掉),
点重合舍掉),![]()
![]()
∵![]() ,
,
∵![]() ,
,
∴PC∥x轴,
∵QP1⊥PC,
∴在Rt△PP1Q中,PP1= ![]() ,QP1=
,QP1= ![]()
![]() 利用勾股定理得:
利用勾股定理得:![]()


科目:初中数学 来源: 题型:
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧![]() 的中点.
的中点.
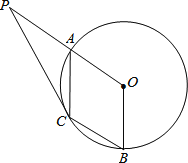
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至P,使得AP=OA,连接PC,若PC为![]() ,求BC长.
,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受非洲猪瘟影响,2019 年肉价大幅.上涨.某养殖场与2018年相比,生猪出栏数减少![]() 头.平均每头出栏价是2018年的
头.平均每头出栏价是2018年的![]() 倍,销售总额比2018年增加
倍,销售总额比2018年增加![]() .
.
![]() 若养殖场2018年生猪销售额为
若养殖场2018年生猪销售额为![]() 万元,求2019年平均每头生猪的出栏价格.
万元,求2019年平均每头生猪的出栏价格.
![]() 一猪肉专营店在5月份经营中,售价为
一猪肉专营店在5月份经营中,售价为![]() 元
元![]() 天可卖
天可卖![]() .6月份每千克上涨
.6月份每千克上涨![]() 元,则
元,则![]() 天少卖
天少卖![]() .受产业链影响继续涨价,销量继续递减.若猪肉的成本折算为
.受产业链影响继续涨价,销量继续递减.若猪肉的成本折算为![]() 元
元![]() 专营店平均每天规划毛利约
专营店平均每天规划毛利约![]() 元,求这家专营店
元,求这家专营店![]() 天为养殖场赚的最大毛利.
天为养殖场赚的最大毛利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 与
与![]() 的平分线,
的平分线,![]() 的延长线与
的延长线与![]() 相交于点
相交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
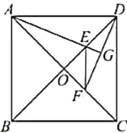
A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的一个交点为点
轴的一个交点为点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() ,抛物线的对称轴
,抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,点
,点![]() 是对称轴
是对称轴![]() 上一动点.
上一动点.

(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
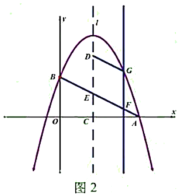
(3)如图2,抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,当四边形
,当四边形![]() 是平行四边形且周长最大时,求出点
是平行四边形且周长最大时,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄山毛峰是中国十大名茶之一 ,产于安徽省黄山(徽州)一带,也称徽茶.有诗日:“未见黄山面,十里闻茶香”.某茶庄以![]() 元
元![]() 的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的
的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的![]() 倍,经试销过发现,日销量
倍,经试销过发现,日销量![]() 与销售单价
与销售单价![]() 的对应关系如下表:且
的对应关系如下表:且![]() 与
与![]() 满足初中所学某种函数关系.
满足初中所学某种函数关系.
|
|
|
|
| ··· |
|
|
|
|
| ··· |
(1)根据表格,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)在销售过程中,每日还需支付其他费用![]() 元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?
元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
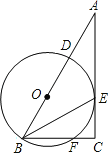
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次学科测验,学生得分均为整数,满分为10分,成绩达到6分以上(包括6
分)为合格,成绩达到9分为优秀.这次测验甲、乙两组学生成绩分布的条形统计图如下:
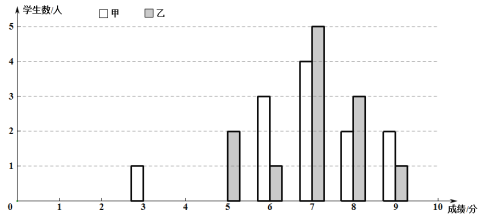
(1)请补充完成下面的成绩统计分析表:

(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组.请你给出三条支持乙组学生观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com