
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧![]() 的中点.
的中点.
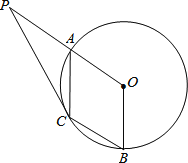
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至P,使得AP=OA,连接PC,若PC为![]() ,求BC长.
,求BC长.
【答案】(1)四边形OACB是菱形,见解析;(2)3
【解析】
(1)首先连接OC,由A、B是圆O上的两点,∠AOB=120°,C是劣弧![]() 的中点,易证得△AOC与△BOC都是等边三角形,则可得AC=OA=OC=OB=BC,继而证得四边形OACB是菱形.
的中点,易证得△AOC与△BOC都是等边三角形,则可得AC=OA=OC=OB=BC,继而证得四边形OACB是菱形.
(2)由AP=OA,易证得△OPC是直角三角形,然后利用勾股定理求得答案.
解:(1)四边形OACB是菱形.
理由:连接OC,
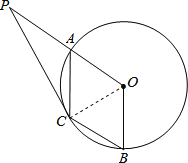
∵∠AOB=120°,C是劣弧![]() 的中点,
的中点,
∴∠AOC=∠BOC=![]() ∠AOB=60°,
∠AOB=60°,
∵OA=OC=OB,
∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,
∴四边形OACB是菱形.
(2)∵AP=OA,AC=OA,
∴AP=AC,
∴∠P=∠ACP=![]() ∠OAC=30°,
∠OAC=30°,
∴∠OCP=90°,
设圆O的半径为x,则OC=x,OP=2x
∴![]() ,
,
∴x=3
∵四边形OACB是菱形.
∴BC=3


科目:初中数学 来源: 题型:
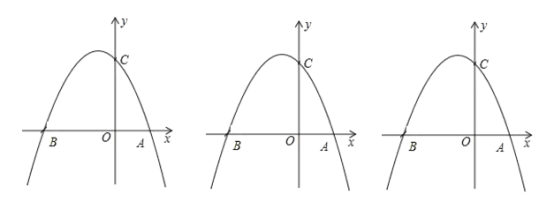
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
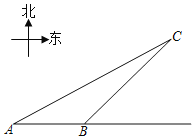
【题目】如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在矩形ABCD对角线AC上由A向C运动,且BC=2![]() ,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
(1)如图1,当AC平分角∠DEF时,求AE的长度;
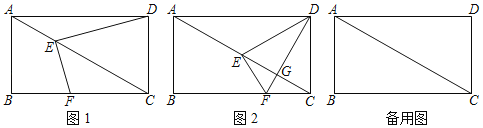
(2)如图2,连结DF,与AC交于点G,若DF⊥AC时,求四边形DEFC的面积;
(3)若点E分AC为1:2两部分时,求BF:FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
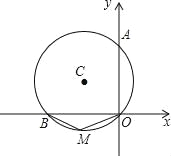
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 为第二象限抛物线上一点,连接
为第二象限抛物线上一点,连接![]() 、
、![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 做
做![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,过点
,过点![]() 做直线
做直线![]() 轴,在
轴,在![]() 轴上方直线
轴上方直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)在(2)的条件下,点![]() 为第二象限抛物线上的一点,连接
为第二象限抛物线上的一点,连接![]() ,过点
,过点![]() 做
做![]() 于点
于点![]() ,连接
,连接![]() ,线段
,线段![]() 、
、![]() 分别交线段
分别交线段![]() 于点
于点![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com