
【题目】如图,点E在矩形ABCD对角线AC上由A向C运动,且BC=2![]() ,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
(1)如图1,当AC平分角∠DEF时,求AE的长度;
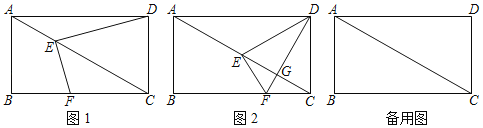
(2)如图2,连结DF,与AC交于点G,若DF⊥AC时,求四边形DEFC的面积;
(3)若点E分AC为1:2两部分时,求BF:FC.
【答案】(1)3﹣![]() ;(2)
;(2)![]() ;(3)BF:CF=4:5或BF:CF=8:1.
;(3)BF:CF=4:5或BF:CF=8:1.
【解析】
(1)如图1中,作DM⊥AC于M,解直角三角形求出CM,EM,AC即可解决问题;
(2)解直角三角形求出DG,FG,CG,利用相似三角形的性质求出EG,根据S四边形DEFC=![]() DFCE求解即可;
DFCE求解即可;
(3)分两种情形:①如图1﹣1中,若AE:CE=1:2,作EM⊥BC于M,EN⊥CD于N.解直角三角形求出EN,DN,EM,再利用相似三角形的性质求出MF即可解决问题.②若AE:CF=2:1时,同法可求.
解:(1)如图1中,作DM⊥AC于M,
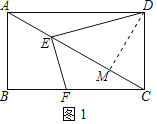
∵四边形ABCD是矩形,
∴∠B=∠BCD=∠ADC=90°,AB=CD,AD=BC=![]() ,
,
∵∠ACB=30°,
∴AB=CD=BCtan30°=2,AC=2AB=4,
在Rt△CDM中,∵∠CMD=90°,∠DCM=60°,CD=2,
∴∠CDM=30°,
∴CM=![]() CD=1,DM=
CD=1,DM=![]() CM=
CM=![]() ,
,
∵∠DEF=90°,EM平分∠DEF,
∴∠DEM=![]() ∠DEF=45°,
∠DEF=45°,
∴EM=DM=![]() ,
,
∴AE=AC﹣EM﹣CM=3﹣![]() ;
;
(2)如图2中,

∵DF⊥AC,
∴∠DGC=90°,
在Rt△CDG中,∵CD=2,∠DCG=60°,
∴∠CDG=30°,
∴CG=![]() CD=1,DG=
CD=1,DG=![]() ,
,
∴FG=CGtan30°=![]() ,
,
∵∠FEG+∠DEG=90°,∠EDG+∠DEG=90°,
∴∠FEG=∠EDG,
∵∠EGF=∠DGE=90°,
∴△EGF∽△DGE,
∴![]() ,
,
∴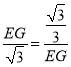 ,
,
∴EG=1,
∴S四边形DEFC=![]() DFCE=
DFCE=![]() ×2×
×2×![]() =
=![]() ;
;
(3)①如图1﹣1中,若AE:CE=1:2,作EM⊥BC于M,EN⊥CD于N.
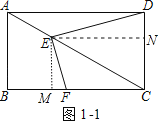
∵AB=CD=2,AC=4,AE:EC=1:2,
∴AE=![]() ,EC=
,EC=![]() ,
,
在Rt△CEN中,∵∠ECN=30°
∴CN=![]() EC=
EC=![]() ,EN=
,EN=![]() CN=
CN=![]() ,
,
∴DN=2﹣![]() =
=![]() ,
,
在Rt△CEM中,∵∠ECM=30°,
∴EM=![]() EC=
EC=![]() ,CM=
,CM=![]() EM=
EM=![]() ,
,
∵DE⊥EF,
∴∠DEF=∠NEM=90°,
∴∠DEN=∠MEF,
∵∠END=∠EMF=90°,
∴△END∽△EMF,
∴![]() ,可得MF=
,可得MF=![]() ,
,
∴CF=CM﹣MF=![]() ,BF=
,BF=![]() ﹣CF=
﹣CF=![]() ,
,
∴BF:CF=4:5;
②若AE:CF=2:1时,同法可得BF:CF=8:1.
综上所述,BF:CF=4:5或BF:CF=8:1.


科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.为了了解垃圾分类知识的普及情况,某校随机调查了部分学生,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制成下面两幅不完整的统计图:
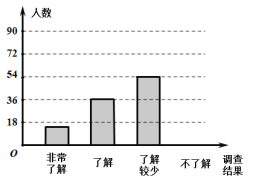
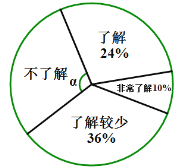
(1)本次被调查的学生有 名,扇形统计图中,![]()
(2)将条形统计图剩余的部分补充完整(包括朱标记的数据)
(3)估计该校![]() 名学生中“非常了解”与“了解”的人数和是多少.
名学生中“非常了解”与“了解”的人数和是多少.
(4)某环保小队有3名男生,1名女生,从中随机抽取2人在全校做垃圾分类知识交流,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
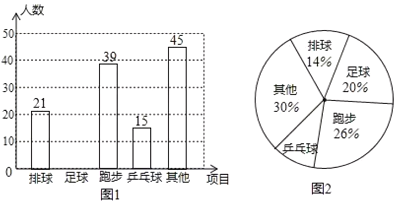
【题目】某校开展“我最喜欢的一项体育社团活动”调查,若每名学生必选且只能选一项,现随机抽查了![]() 名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
(1)求![]() 的值;
的值;
(2)补全条形统计图;
(3)求“乒乓球”所对应的扇形圆心角的度数;
(4)已知该校共有2400名学生,请你估计该校学生最喜欢篮球社团活动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
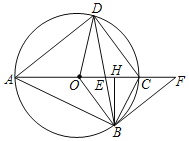
【题目】如图,四边形ABCD内接于⊙O,直径AC与弦BD的交点为E,OB∥CD,BH⊥AC,垂足为H,且∠BFA=∠DBC.
(1)求证:BF是⊙O的切线;
(2)若BH=3,求AD的长度;
(3)若sin∠DAC=![]() ,求△OBH的面积与四边形OBCD的面积之比.
,求△OBH的面积与四边形OBCD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧![]() 的中点.
的中点.
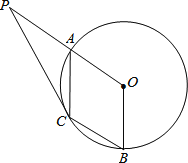
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至P,使得AP=OA,连接PC,若PC为![]() ,求BC长.
,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,如图记录了跑的最快的一位选手与最慢的一位选手的跑步过程(最快的选手跑完了全程),其中x表示最快的选手的跑步时间,y表示这两位选手之间的距离,现有以下4种说法,正确的有( )
①最快的选手到达终点时,最慢的选手还有15米未跑;
②跑的最快的选手用时4'46″;
③出发后最快的选手与最慢的选手相遇了两次;
④出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时长.
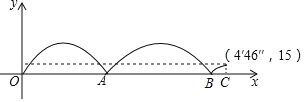
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的一个交点为点
轴的一个交点为点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() ,抛物线的对称轴
,抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,点
,点![]() 是对称轴
是对称轴![]() 上一动点.
上一动点.

(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)如图2,抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,当四边形
,当四边形![]() 是平行四边形且周长最大时,求出点
是平行四边形且周长最大时,求出点![]() 的横坐标.
的横坐标.
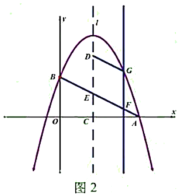
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com