
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.为了了解垃圾分类知识的普及情况,某校随机调查了部分学生,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制成下面两幅不完整的统计图:
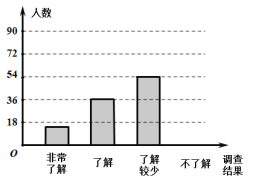
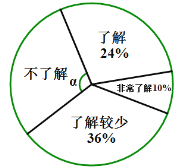
(1)本次被调查的学生有 名,扇形统计图中,![]()
(2)将条形统计图剩余的部分补充完整(包括朱标记的数据)
(3)估计该校![]() 名学生中“非常了解”与“了解”的人数和是多少.
名学生中“非常了解”与“了解”的人数和是多少.
(4)某环保小队有3名男生,1名女生,从中随机抽取2人在全校做垃圾分类知识交流,求恰好抽到一男一女的概率.
【答案】(1)![]() ;(2)见解析;(3)952;(4)树状图见解析,
;(2)见解析;(3)952;(4)树状图见解析,![]()
【解析】
(1)先由了解的人数及其所占百分比求出总人数,再根据各项目的百分比之和为1求出不了解对应的百分比,用360°乘以不了解对应的百分比可得答案;
(2)用总人数分别乘以非常了解、了解较少、不了解对应的百分比求出其人数,据此可补全图形;
(3)用总人数乘以两者百分比之和即可得;
(4)画树状图展示所有12种等可能的结果数,找出抽到一男一女的结果数,然后根据概率公式求解.
(1)本次被调查的学生有36÷24%=150(名),
∵“不了解”对应的百分比为1-(24%+10%+36%)=30%,
∴扇形统计图中,∠α=360°×30%=108°,
故答案为:150、108°;
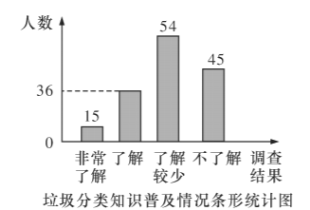
(2)非常了解的人数为150×10%=15(名),
了解较少的人数为150×36%=54(名),
不了解的人数为150×30%=45(名),
补全图形如下:
![]() 估计该校
估计该校![]() 名学生中“非常了解”与“了解”的人数和是
名学生中“非常了解”与“了解”的人数和是![]() (名);
(名);
![]() 可以画树状图为:
可以画树状图为:
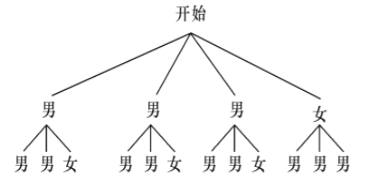
共有![]() 种等可能的结果,其中抽到
种等可能的结果,其中抽到![]() 男
男![]() 女的结果数为
女的结果数为![]()
所以恰好抽到一男一女的概率为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
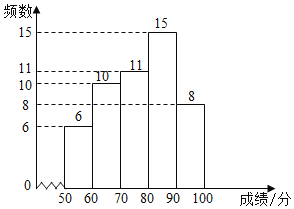
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:
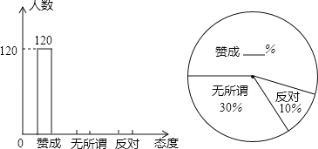
根据上述信息,解答下列问题:
(1)抽取的学生人数为 ;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把函数![]() 的图像绕点
的图像绕点![]() 旋转180°,得到新函数
旋转180°,得到新函数![]() 的图像,我们称
的图像,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图像的对称轴为直线
的图像的对称轴为直线![]() .例如:当
.例如:当![]() 时,函数
时,函数![]() 关于点
关于点![]() 的相关函数为
的相关函数为![]() .
.
(1)填空:![]() 的值为________(用含
的值为________(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,
时,![]() 的图像与
的图像与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 绕原点
绕原点![]() 顺时针旋转90°,得到它的对应线段
顺时针旋转90°,得到它的对应线段![]() .若线段
.若线段![]() 与
与![]() 的图像有公共点,结合函数图像,求
的图像有公共点,结合函数图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
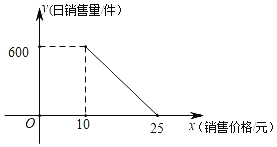
【题目】奏响复工复产“协奏曲”,防疫复产两不误.2020年2月5日,四川省出台《关于应对新型冠状病毒肺炎疫情缓解中小企业生产经营困难的政策措施》,推出减负降成本、破解融资难、财政补贴和税收减免、稳岗支持等13条举措,携手中小企业共渡难关.某企业积极复工复产,生产某种产品成本为9元/件,经过市场调查获悉,日销售量y(件)与销售价格x(元/件)的函数关系如图所示:
(1)求出y与x之间的函数表达式;
(2)当销售价格为多少元时,该企业日销售额为6000元?
(3)若该企业每销售1件产品可以获得2元财政补贴,则当销售价格x为何值时,该企业可以获最大日利润,最大日利润值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
上课时孙老师提出这样一个问题:对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
小明的思路是:原不等式等价于![]() ,设函数
,设函数![]() ,
,![]() ,画出两个函数的图象的示意图,于是原问题转化为函数
,画出两个函数的图象的示意图,于是原问题转化为函数![]() 的图象在
的图象在![]() 的图象上方时
的图象上方时![]() 的取值范围.
的取值范围.

请结合小明的思路回答:
对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是_____.
的取值范围是_____.
参考小明思考问题的方法,解决问题:
关于![]() 的方程
的方程![]() 在
在![]() 范围内有两个解,求
范围内有两个解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
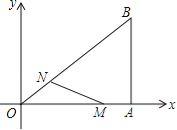
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在矩形ABCD对角线AC上由A向C运动,且BC=2![]() ,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
(1)如图1,当AC平分角∠DEF时,求AE的长度;
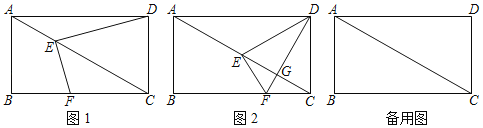
(2)如图2,连结DF,与AC交于点G,若DF⊥AC时,求四边形DEFC的面积;
(3)若点E分AC为1:2两部分时,求BF:FC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com