
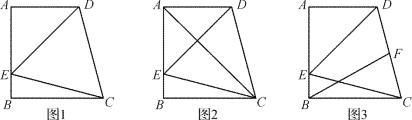
【题目】如图1所示,在四边形ABCD中,AD∥BC, AB⊥BC,∠DCB=75,以CD为一边的等边△DCE的另一顶点E在边AB上.
(1)求∠AED的度数;
(2)连接AC,如图2所示,试判断△ABC的形状;
(3)如图3所示,若F为线段CD上一点,AB=4,∠FBC=30,求DF的长.
【答案】(1) 45°;(2)△ABC的形状是等腰直角三角形,理由见解析;(3) ![]()
【解析】
(1)根据直线平行的性质得到∠ADC的度数,再根据等边三角形的性质和AB⊥BC即可得到答案;
(2)先证A在线段DE的垂直平分线上,再证明点C也在线段DE的垂直平分线上,最后得到BA=BC,即可得到△ABC的形状;
(3) 连接AF,BF、AD的延长线交于点G,证△BCF≌△GDF(ASA)得到DF=CF,再根据三角函数值计算即可得到答案;
解:(1)∵∠DCB=75,AD∥BC,
∴∠ADC=180°-75°=105°(两直线平行,同旁内角互补),
又∵△DCE是等边三角形,
∴∠CDE=60°,
故∠ADE=105°-60°=45°,
又∵AD∥BC, AB⊥BC,
∴∠DAB=90°,
∴∠AED=180°-90°-45°=45°;
(2) 由(1)知∠AED=45°,
∴AD=AE,
故点A在线段DE的垂直平分线上,
又∵△DCE是等边三角形,
∴CD=CE,
故点C也在线段DE的垂直平分线上,
∴AC就是线段DE的垂直平分线,即AC⊥DE,
∵∠AED=45°,
∴∠BAC=45°,
又∵AB⊥BC,
∴BA=BC,
故△ABC的是等腰直角三角形;
(3) 连接AF,BF、AD的延长线交于点G,如下图:

∵∠FBC=30,∠DCB=75,
∴∠BFC=75°,
∴BC=BF,
又由(2)知BA=BC,
∴BF=BC(等量替换),
∴∠ABF=90°-30°=60°,
∴AB=BF=FA,
又∵AD∥BC, AB⊥BC,
∴∠FAG=∠G=30°,
∴FG=FA=FB,
∵∠G=∠FBC=30°,∠DFG=∠CFB,FB=FG,
∴△BCF≌△GDF(ASA),
∴DF=CF,
又∵根据题意得: ,
,
我们知道![]() ,
,
∴ ,
,
∴DF=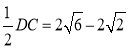 ;
;


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
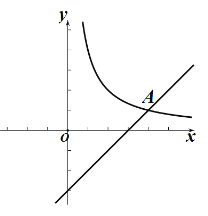
【题目】如图,在平面直角坐标系xOy中,函数![]() (k>0)的图象与直线y=x-3相交与点A(4,m).
(k>0)的图象与直线y=x-3相交与点A(4,m).
(1)求k、m的值;
(2)已知点P(a,a)(a>0),过点P作垂直于y轴的直线,交直线y=x-3于点M,过点P作垂直于x轴的直线,交函数![]() (k>0)的图象于点N.
(k>0)的图象于点N.
①当a=1时,判断PM与PN之间的数量关系,并说明理由;
②若PM≥PN,请结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
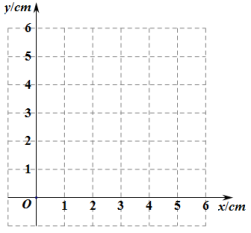
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:

(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:有代数式①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .若从中随机抽取两个,用“=”连接.
.若从中随机抽取两个,用“=”连接.
(1)写出能得到的一元二次方程;
(2)从(1)中得到的一元二次方程中挑选一个进行解方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
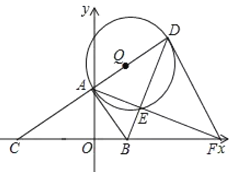
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,点B是
,点B是![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,过点A作
,过点A作![]() ,交
,交![]() 轴于点C,点D是点C关于点A的对称点,连接
轴于点C,点D是点C关于点A的对称点,连接![]() ,以
,以![]() 为直径作
为直径作![]() 交
交![]() 于点E,连接AE并延长交
于点E,连接AE并延长交![]() 轴于点F,连接DF.
轴于点F,连接DF.
(1)求线段AE的长;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 与
与![]() 相似,求
相似,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销甲、乙两种商品![]() 现有如下信息:信息1:甲、乙两种商品的进货单价之和是3元;信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元;信息3:按零售单价购买甲商品3件和乙商品2件,共付了12元.请根据以上信息,解答下列问题:
现有如下信息:信息1:甲、乙两种商品的进货单价之和是3元;信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元;信息3:按零售单价购买甲商品3件和乙商品2件,共付了12元.请根据以上信息,解答下列问题:
![]() 求甲、乙两种商品的零售单价;
求甲、乙两种商品的零售单价;
![]() 该商店平均每天卖出甲商品500件和乙商品1200件
该商店平均每天卖出甲商品500件和乙商品1200件![]() 经调查发现,甲种商品零售单价每降
经调查发现,甲种商品零售单价每降![]() 元,甲种商品每天可多销售100件
元,甲种商品每天可多销售100件![]() 商店决定把甲种商品的零售单价下降
商店决定把甲种商品的零售单价下降![]() 元
元![]() 在不考虑其他因素的条件下,当m为多少时,商店每天销售甲、乙两种商品获取的总利润为1700元?
在不考虑其他因素的条件下,当m为多少时,商店每天销售甲、乙两种商品获取的总利润为1700元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0),经过点(1.0),对称轴l如图所示,若M=a+b﹣c,N=2a﹣b,P=a+c,则M,N,P中,值小于0的数有( )个.
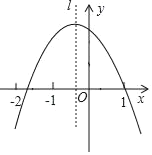
A.2B.1C.0D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,其中a>0.
,其中a>0.
(1)若方程![]() 有两个实根
有两个实根![]() ,且方程
,且方程![]() 有两个相等的实根,求二次函数的解析式;
有两个相等的实根,求二次函数的解析式;
(2)若二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,且当
两点,且当![]() 时,
时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com