
【题目】如图,点A(﹣2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线y=![]() (k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )
(k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )
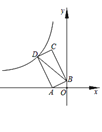
A.﹣9B.﹣12C.﹣16D.﹣18
【答案】C
【解析】
过D作DM⊥x轴于M,根据相似三角形的性质和判定求出DM=2AM,根据三角形的面积求出AM,即可求出DM和OM,得出答案即可.
解:
∵点A(-2,0),B(0,1),
∴OA=2,OB=1,
过D作DM⊥x轴于M,则∠DMA=90°,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠DMA=∠DAB=∠AOB=90°,
∴∠DAM+∠BAO=90°,∠DAM+∠ADM=90°,
∴∠ADM=∠BAO,
∴△DMA∽△AOB,
∴![]() =2,
=2,
即DM=2MA,
设AM=x,则DM=2x,
∵四边形OADB的面积为6,
∴S梯形DMOB-S△DMA=6,
∴![]() (1+2x)(x+2)-
(1+2x)(x+2)-![]() 2xx=6,
2xx=6,
解得:x=2,
则AM=2,OM=4,DM=4,
即D点的坐标为(-4,4),
∴k=-4×4=-16,
故选C.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+![]() x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某中学开展了周末网课学习活动,为了解学生网课学习效果进行了抽样测试,该校教导处把测试结果分为A(优秀)、B(良好)、C(不合格)三种类型.如图是对该校初一(1)班和初一(2)班全体同学进行测试后绘制的两幅不完整的统计图,请根据图中信息解答下列问题.
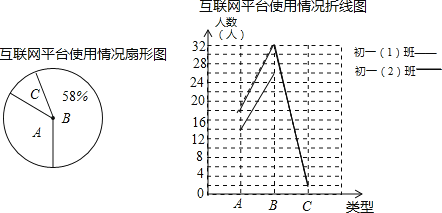
(1)此次被调查的学生总人数是 人;扇形统计图中代表类型C的扇形的圆心角为 ;
(2)补全折线统计图;
(3)如果该校初一年级学生共有1200人,试根据此次调查结果估计该校初一年级中C类学生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
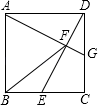
(1)证明:△ADG≌△DCE;(2)连接BF,证明:AB=FB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
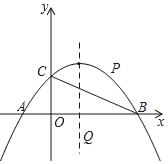
【题目】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
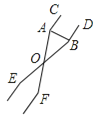
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使PC是⊙O的切线.
(1)求证:∠PCA=∠ABC;
(2)若∠P=60°,PC=4,求PE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一种雪球夹的简化结构图,其通过一个固定夹体和一个活动夹体的配合巧妙地完成夹雪、投雪的操作,不需人手直接接触雪,使用方便,深受小朋友的喜爱.当雪球夹闭合时,测得∠AOB=30°,OA=OB=14 cm,则此款雪球夹制作的雪球的直径AB的长度为________ cm.(结果保留一位小数.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
查看答案和解析>>
科目:初中数学 来源: 题型:
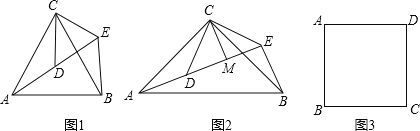
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为 ;
②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,CD=3,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com