
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
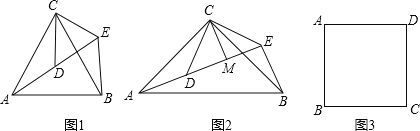
ШчЭМ1ЃЌЁїACBКЭЁїDCEОљЮЊЕШБпШ§НЧаЮЃЌЕуAЃЌDЃЌEдкЭЌвЛжБЯпЩЯЃЌСЌНгBEЃЎ
ЬюПеЃК
ЂйЁЯAEBЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЂкЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉЭиеЙЬНОП
ШчЭМ2ЃЌЁїACBКЭЁїDCEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=ЁЯDCE=90ЁуЃЌЕуAЃЌDЃЌEдкЭЌвЛжБЯпЩЯЃЌCMЮЊЁїDCEжаDEБпЩЯЕФИпЃЌСЌНгBEЃЌЧыХаЖЯЁЯAEBЕФЖШЪ§МАЯпЖЮCMЃЌAEЃЌBEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉНтОіЮЪЬт
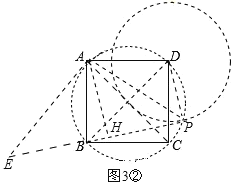
ШчЭМ3ЃЌдке§ЗНаЮABCDжаЃЌCD=3ЃЌШєЕуPТњзуPD=1ЃЌЧвЁЯBPD=90ЁуЃЌЧыжБНгаДГіЕуAЕНBPЕФОрРыЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй60ЁуЃЛЂкAD=BEЃЛЃЈ2ЃЉЁЯAEB=90ЁуЃЌAE=BE+2CMЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬѕМўвзжЄЁїACDЁеЁїBCEЃЌДгЖјЕУЕНЃКAD=BEЃЌЁЯADC=ЁЯBECЃЎгЩЕуAЃЌDЃЌEдкЭЌвЛжБЯпЩЯПЩЧѓГіЁЯADCЃЌДгЖјПЩвдЧѓГіЁЯAEBЕФЖШЪ§ЃЎ
ЃЈ2ЃЉЗТееЃЈ1ЃЉжаЕФНтЗЈПЩЧѓГіЁЯAEBЕФЖШЪ§ЃЌжЄГіAD=BEЃЛгЩЁїDCEЮЊЕШбќжБНЧШ§НЧаЮМАCMЮЊЁїDCEжаDEБпЩЯЕФИпПЩЕУCM=DM=MEЃЌДгЖјжЄЕНAE=2CH+BEЃЎ
ЃЈ3ЃЉгЩPD=1ПЩЕУЃКЕуPдквдЕуDЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЩЯЃЛгЩЁЯBPD=90ЁуПЩЕУЃКЕуPдквдBDЮЊжБОЖЕФдВЩЯЃЎЯдШЛЃЌЕуPЪЧетСНИідВЕФНЛЕуЃЌгЩгкСНдВгаСНИіНЛЕуЃЌНгЯТРДашЖдСНИіЮЛжУЗжБ№НјааЬжТлЃЎШЛКѓЃЌЬэМгЪЪЕБЕФИЈжњЯпЃЌНшжњгкЃЈ2ЃЉжаЕФНсТлМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉ![]() ЁЯACB=ЁЯDCEЃЌЁЯDCB=ЁЯDCB
ЁЯACB=ЁЯDCEЃЌЁЯDCB=ЁЯDCB
![]() ЁЯACD=ЁЯBCE
ЁЯACD=ЁЯBCE
дкЁїACDКЭЁїBCEжа
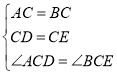
![]()
![]() AD=BEЃЌЁЯCEB=ЁЯADC=180Ёу-ЁЯCDE=120Ёу
AD=BEЃЌЁЯCEB=ЁЯADC=180Ёу-ЁЯCDE=120Ёу
![]() ЁЯAEB=ЁЯCEB-ЁЯCED=60Ёу.
ЁЯAEB=ЁЯCEB-ЁЯCED=60Ёу.
ЂкЁпЁїACDЁеЁїBCEЃЌЁрAD=BEЃЎД№АИЮЊЃКAD=BEЃЎ
ЃЈ2ЃЉЁЯAEB=90ЁуЃЌAE=BE+2CMЃЎ
РэгЩЃКШчЭМ 2ЃЌ
ЁпЁїACB КЭЁїDCE ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCA=CBЃЌCD=CEЃЌЁЯACB=ЁЯDCE=90ЁуЃЎ
ЁрЁЯACD=ЁЯBCEЃЎ
дкЁїACD КЭЁїBCE жаЃЌ
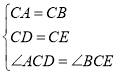
ЁрЁїACDЁеЁїBCEЃЎЁрAD=BEЃЌЁЯADC=ЁЯBECЃЎ
ЁпЁїDCE ЮЊЕШбќжБНЧШ§НЧаЮЃЌЁрЁЯCDE=ЁЯCED=45ЁуЃЎ
ЁпЕу AЃЌDЃЌE дкЭЌвЛжБЯпЩЯЃЌЁрЁЯADC=135ЁуЃЎ
ЁрЁЯBEC=135ЁуЃЎЁрЁЯAEB=ЁЯBECЉЁЯCED=90ЁуЃЎ
ЁпCD=CEЃЌCMЁЭDEЃЌЁрDM=MEЃЎ
ЁпЁЯDCE=90ЁуЃЌЁрDM=ME=CMЃЎ
ЁрAE=AD+DE=BE+2CMЃЎ
ЃЈ3ЃЉЕуAЕНBPЕФОрРыЮЊ![]() Лђ
Лђ![]()
РэгЩШчЯТЃК
ЁпPD=1ЃЌ
ЁрЕуPдквдЕуDЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЩЯЁЃ
ЁпЁЯBPD=90ЃЌ
ЁрЕуPдквдBDЮЊжБОЖЕФдВЩЯЁЃ
ЁрЕуPЪЧетСНдВЕФНЛЕуЁЃ
ЂйЕБЕуPдкШчЭМ3ЂйЫљЪОЮЛжУЪБЃЌ
СЌНгPDЁЂPBЁЂPA,зїAHЁЭBP,ДЙзуЮЊH,
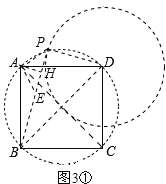
Й§ЕуAзїAEЁЭAPЃЌНЛBPгкЕуEЃЌШчЭМ3ЂйЁЃ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯADB=45.AB=AD=DC=BC=3,ЁЯBAD=90.
ЁрBD=2.
ЁпDP=1ЃЌ
ЁрBP=![]() .
.
ЁпЁЯBPD=ЁЯBAD=90ЃЌ
ЁрAЁЂPЁЂD. BдквдBDЮЊжБОЖЕФдВЩЯЃЌ
ЁрЁЯAPB=ЁЯADB=45.
ЁрЁїPAEЪЧЕШбќжБНЧШ§НЧаЮЁЃ
гжЁпЁїBADЪЧЕШбќжБНЧШ§НЧаЮЃЌЕуB. E. PЙВЯпЃЌAHЁЭBPЃЌ
ЁргЩ(2)жаЕФНсТлПЩЕУЃКBP=2AH+PD.
Ёр![]() =2AH+1.
=2AH+1.
ЁрAH=![]() .
.
ЂкЕБЕуPдкШчЭМ3ЂкЫљЪОЮЛжУЪБЃЌ
СЌНгPDЁЂPBЁЂPAЃЌзїAHЁЭBPЃЌДЙзуЮЊHЃЌ
Й§ЕуAзїAEЁЭAPЃЌНЛPBЕФбгГЄЯпгкЕуEЃЌШчЭМ3ЂкЁЃ
ЭЌРэПЩЕУЃКBP=2AHPD.
Ёр![]() =2AH1.
=2AH1.
ЁрAH=![]() .
.
злЩЯЫљЪіЃКЕуAЕНBPЕФОрРыЮЊ![]() Лђ
Лђ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
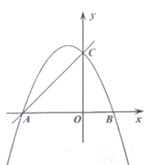
ЁОЬтФПЁПШчЭМЃЌЕуAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ1ЃЉЃЌвдЯпЖЮABЮЊБпдкЕкЖўЯѓЯозїОиаЮABCDЃЌЫЋЧњЯпyЃН![]() ЃЈkЃМ0ЃЉЙ§ЕуDЃЌСЌНгBDЃЌШєЫФБпаЮOADBЕФУцЛ§ЮЊ6ЃЌдђkЕФжЕЪЧЃЈ ЃЉ
ЃЈkЃМ0ЃЉЙ§ЕуDЃЌСЌНгBDЃЌШєЫФБпаЮOADBЕФУцЛ§ЮЊ6ЃЌдђkЕФжЕЪЧЃЈ ЃЉ
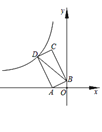
A.Љ9B.Љ12C.Љ16D.Љ18
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыЗНЯђа§зЊ
ЫГЪБеыЗНЯђа§зЊ![]() ЕН
ЕН![]() ЕФЮЛжУЃЌСЌНг
ЕФЮЛжУЃЌСЌНг![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃП
ЕФГЄЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
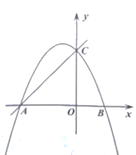
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈ1ЃЌ2ЃЉЃЌBЃЈ1ЃЌЉ1ЃЉЃЌCЃЈ2ЃЌ2ЃЉЃЌХзЮяЯпyЃНax2ЃЈaЁй0ЃЉОЙ§ЁїABCЧјгђЃЈАќРЈБпНчЃЉЃЌдђaЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
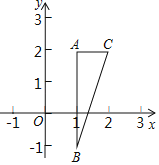
A.aЁмЉ1ЛђaЁн2B.![]() ЁмaЁм2
ЁмaЁм2
C.Љ1ЁмaЃМ0Лђ1ЃМaЁм![]() D.Љ1ЁмaЃМ0Лђ0ЃМaЁм2
D.Љ1ЁмaЃМ0Лђ0ЃМaЁм2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЫШЄаЁзщЮЊСЫСЫНтБОаЃФаЩњВЮМгПЮЭтЬхг§ЖЭСЖЧщПіЃЌЫцЛњГщШЁБОаЃ300УћФаЩњНјааСЫЮЪОэЕїВщЃЌЭГМЦећРэВЂЛцжЦСЫШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЎ
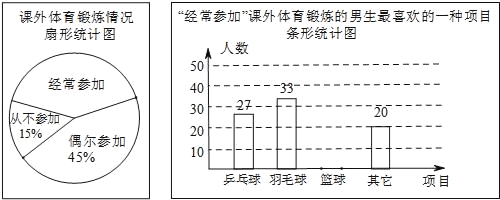
ЧыИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉПЮЭтЬхг§ЖЭСЖЧщПіЩШаЮЭГМЦЭМжаЃЌЁАОГЃВЮМгЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЮЊ________ЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУаЃЙВга1200УћФаЩњЃЌЧыЙРМЦШЋаЃФаЩњжаОГЃВЮМгПЮЭтЬхг§ЖЭСЖВЂЧвзюЯВЛЖЕФЯюФПЪЧРКЧђЕФШЫЪ§ЃЛ
ЃЈ4ЃЉаЁУїШЯЮЊЁАШЋаЃЫљгаФаЩњжаЃЌПЮЭтзюЯВЛЖВЮМгЕФдЫЖЏЯюФПЪЧЦЙХвЧђЕФШЫЪ§дМЮЊ1200ЁС![]() =108ЁБЃЌЧыФуХаЖЯетжжЫЕЗЈЪЧЗёе§ШЗЃЌВЂЫЕУїРэгЩЃЎ
=108ЁБЃЌЧыФуХаЖЯетжжЫЕЗЈЪЧЗёе§ШЗЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪЎАЫДѓвдРДЃЌФГаЃвбОйАьЮхНьаЃдАвеЪѕНк.ЮЊСЫКыбяжаЛЊгХауДЋЭГЮФЛЏЃЌУПНьвеЪѕНкЩЯЖМгавЛаЉАрМЖБэбнЁАОЕфЫаЖСЁБЁЂЁАУёРжбнзрЁБЁЂЁАИшЧњСЊГЊЁБЁЂЁАУёзхЮшЕИЁБЕШНкФП.аЁгБЖдУПНьвеЪѕНкБэбнетаЉНкФПЕФАрМЖЪ§НјааЭГМЦЃЌВЂЛцжЦСЫШчЭМЫљЪОВЛЭъећЕФелЯпЭГМЦЭМКЭЩШаЮЭГМЦЭМ.
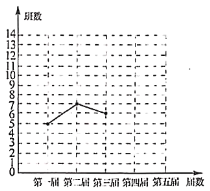
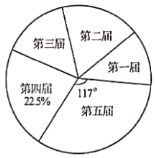
(1)ЮхНьвеЪѕНкЙВга________ИіАрМЖБэбнетаЉНкШеЃЌАрЪ§ЕФжаЮЛЪ§ЮЊ________ЃЌдкЩШаЮЭГМЦЭМжаЃЌЕкЫФНьАрМЖЪ§ЕФЩШаЮдВаФНЧЕФЖШЪ§ЮЊ________ЃЛ
(2)ВЙШЋелЯпЭГМЦЭМЃЛ
(3)ЕкСљНьвеЪѕНкЃЌФГАрОіЖЈДгетЫФЯювеЪѕаЮЪНжаШЮбЁСНЯюБэбн(ЁАОЕфЫаЖСЁБЁЂЁАУёРжбнзрЁБЁЂЁАИшЧњСЊГЊЁБЁЂЁАУёзхЮшЕИЁБЗжБ№гУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() БэЪО).РћгУЪїзДЭМЛђБэИёЧѓГіИУАрбЁдё
БэЪО).РћгУЪїзДЭМЛђБэИёЧѓГіИУАрбЁдё![]() КЭ
КЭ![]() СНЯюЕФИХТЪ.
СНЯюЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌХзЮяЯп
СНЕуЃЌХзЮяЯп![]() ОЙ§
ОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсЕФСэвЛИіНЛЕуЮЊ
жсЕФСэвЛИіНЛЕуЮЊ![]() ЃЌЧв
ЃЌЧв![]() .
.
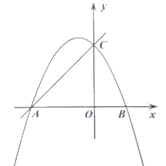
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() дк
дк![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЌЧв
ЕФбгГЄЯпЩЯЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊЕквЛЯѓЯоФкЕФвЛЕуЃЌЕБ
ЮЊЕквЛЯѓЯоФкЕФвЛЕуЃЌЕБ![]() ЪЧвд
ЪЧвд![]() ЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЪБЃЌСЌНг
ЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЪБЃЌСЌНг![]() ЃЌЩш
ЃЌЩш![]() ЕФГЄЖШЮЊ
ЕФГЄЖШЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧыгУКЌ
ЃЌЧыгУКЌ![]() ЕФЪНзгБэЪО
ЕФЪНзгБэЪО![]() ЃЌВЂаДГіздБфСП
ЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() ЗелЕН
ЗелЕН![]() ЕФЮЛжУЃЈ
ЕФЮЛжУЃЈ![]() гы
гы![]() ЖдгІЃЉЃЌШє
ЖдгІЃЉЃЌШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
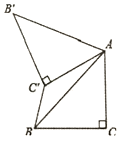
ЁОЬтФПЁПШчЭМЃЌдке§Ш§НЧаЮABCжаЃЌЕуDЁЂEЗжБ№дкACЁЂABЩЯЃЌЧв![]() ЃЌAE=BEЃЌдђгаЃЈ ЃЉ
ЃЌAE=BEЃЌдђгаЃЈ ЃЉ
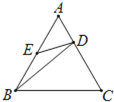
A.ЁїAEDЁзЁїBEDB.ЁїAEDЁзЁїCBD
C.ЁїAEDЁзЁїABDD.ЁїBADЁзЁїBCD
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
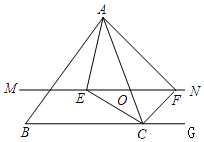
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЕуOЪЧACБпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуOзїжБЯп
жаЃЌЕуOЪЧACБпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуOзїжБЯп![]() ЃЌЩшMNНЛ
ЃЌЩшMNНЛ![]() ЕФНЧЦНЗжЯпгкЕуEЃЌНЛ
ЕФНЧЦНЗжЯпгкЕуEЃЌНЛ![]() ЕФЭтНЧЦНЗжЯпгкЕуFЃЎ
ЕФЭтНЧЦНЗжЯпгкЕуFЃЎ
![]() ЧѓжЄЃК
ЧѓжЄЃК![]() ЃЛ
ЃЛ
![]() ЕБЕуOдЫЖЏЕНКЮДІЪБЃЌЫФБпаЮAECFЪЧОиаЮЃПЧыЫЕУїРэгЩЃЛ
ЕБЕуOдЫЖЏЕНКЮДІЪБЃЌЫФБпаЮAECFЪЧОиаЮЃПЧыЫЕУїРэгЩЃЛ
![]() дк
дк![]() ЕФЬѕМўЯТЃЌИј
ЕФЬѕМўЯТЃЌИј![]() дйЬэМгвЛИіЬѕМўЃЌЪЙЫФБпаЮAECFЪЧе§ЗНаЮЃЌФЧУДЬэМгЕФЬѕМўЪЧ______ЃЎ
дйЬэМгвЛИіЬѕМўЃЌЪЙЫФБпаЮAECFЪЧе§ЗНаЮЃЌФЧУДЬэМгЕФЬѕМўЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com