
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.
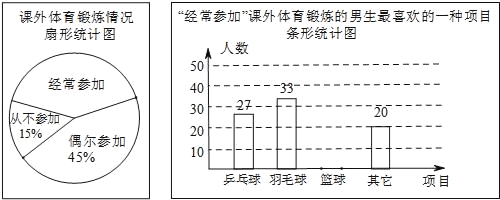
请根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为________;
(2)请补全条形统计图;
(3)该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
(4)小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1200×![]() =108”,请你判断这种说法是否正确,并说明理由.
=108”,请你判断这种说法是否正确,并说明理由.
【答案】(1)144°;(2)见解析;(3)160人;(4)不正确,理由见解析.
【解析】
试题分析:(1)360°×(1﹣15%﹣45%)=360°×40%=144°;故答案为:144°;
(2)“经常参加”的人数为:300×40%=120人,喜欢篮球的学生人数为:120﹣27﹣33﹣20=120﹣80=40人;补全统计图如图所示;
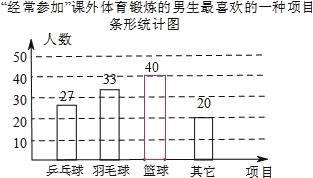
(3)全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为:1200×![]() =160人;
=160人;
(4)这个说法不正确.理由如下:小明得到的108人是经常参加课外体育锻炼的男生中最喜欢的项目是乒乓球的人数,而全校偶尔参加课外体育锻炼的男生中也会有最喜欢乒乓球的,因此应多于108人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
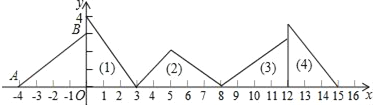
【题目】如图,在平面直角坐标系中,已知点A(﹣4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(5)个三角形的直角顶点的坐标是_____,第(2018)个三角形的直角顶点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的![]() 倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A,B两种设备每台的成本分别是多少万元?
(2)A,B两种设备每台的售价分别是6万元,10万元,该公司生产两种设备各30台,为更好的支持“一带一路”的战略构想,公司决定优惠卖给“一带一路”沿线的甲国,A种设备按原来售价8折出售,B种设备在原来售价的基础上优惠10%,若设备全部售出,该公司一共获利多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B的坐标是(0,2),动点A从原点O出发,沿着x轴正方向移动,△ABP是以AB为斜边的等腰直角三角形(点A、B、P顺时针方向排列),当点A与原点O重合时,得到等腰直角△OBC(此时点P与点C重合).
(1)BC=______;当OA=2时,点P的坐标是______;
(2)设动点A的坐标为(t,0)(t≥0).
①求证:点A在移动过程中,△ABP的顶点P一定在射线OC上;
②用含t的代数式表示点P的坐标为:(______,______);
(3)过点P做y轴的垂线PQ,Q为垂足,当t=______时,△PQB与△PCB全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )

A. (2017,0) B. (2017![]() ,
, ![]() ) C. (2018,
) C. (2018, ![]() ) D. (2018,0)
) D. (2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 城市在
城市在![]() 城市正东方向,现计划在
城市正东方向,现计划在![]() 两城市间修建一条高速铁路(即线段
两城市间修建一条高速铁路(即线段![]() ),经测量,森林保护区的中心
),经测量,森林保护区的中心![]() 在城市
在城市![]() 的北偏东
的北偏东![]() 方向上,在线段
方向上,在线段![]() 上距
上距![]() 城市
城市![]() 的
的![]() 处测得
处测得![]() 在北偏东
在北偏东![]() 方向上,已知森林保护区是以点
方向上,已知森林保护区是以点![]() 为圆心,
为圆心,![]() 为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED.=EC.
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),请写出AE,AC和CD之间的数量关系,不需要证明;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请写出AE、AC和CD的数量关系,不需要证明;
(4)在(1)和(2)的条件下,若AE=2,CD=6,则AC= 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场销售某种商品,统计发现:每件盈利![]() 元时,平均每天可销售
元时,平均每天可销售![]() 件.经调查发现,该商品每降价
件.经调查发现,该商品每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件.
件.
![]() 假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到
假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到![]() 元,请你帮忙思考,该降价多少?
元,请你帮忙思考,该降价多少?
![]() 假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,AC,BD是对角线,E、F、G、H分别是线段BD、BC、AC、AD上的点,对于四边形EFGH的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )

A. 当E,F,G,H是各条线段的中点时,四边形EFGH为平行四边形
B. 当E,F,G,H是各条线段的中点,且AC⊥BD时,四边形EFGH为矩形
C. 当E,F,G,H是各条线段的中点,且AB=CD时,四边形EFGH为菱形
D. 当E,F,G,H不是各条线段的中点时,四边形EFGH可以为平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com