
【题目】已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.
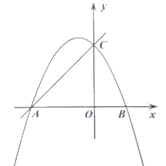
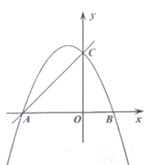
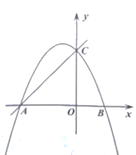
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为第一象限内的一点,当
为第一象限内的一点,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,连接
为斜边的等腰直角三角形时,连接![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并写出自变量
,并写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,连接![]() 、
、![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置(
的位置(![]() 与
与![]() 对应),若
对应),若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() (0<t<4);(3)K(1,-1)
(0<t<4);(3)K(1,-1)
【解析】
(1)利用![]() 求出点C、A的坐标及点B的坐标,即可代入
求出点C、A的坐标及点B的坐标,即可代入![]() 求出解析式;
求出解析式;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,设QF=m,根据△QDF≌△DPE 求出FD=4+t-m,EP=4-t+m,解出m=t ,即可根据三角形的面积公式计算得到函数解析式及t的取值范围;
(3)作PL∥OQ ,GM⊥AB于M ,KN⊥AB于N,证得 △PGL≌△QGC,得到GP=GQ,根据勾股定理求出t,再证明四边形PGDK为正方形,根据正方形的性质及△GMP≌△PNK求出AN及ON即可.
(1)解:当x=0时,y=4,∴C(0,4)
当y=0时,x=-4,∴A(-4,0)
∵OC=2OB,
∴OB=2 ,
∴B(2,0)
代入抛物线解析式得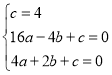 ,
,
解得 ,
,
∴抛物线的解析式为![]() ;
;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,
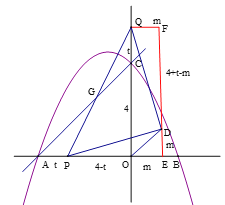
∴四边形QOEF为矩形
∴QF=OE,QO=FE,
设QF=m,
∵△QDF≌△DPE ,
∴QF=DE=m ,FD=EP,
∵FD=4+t-m,EP=4-t+m,
∴4-t+m=4+t-m,
∴m=t ,
∵OP=4-t,
∴![]() (0<t<4),
(0<t<4),
(3)作PL∥OQ ,GM⊥AB于M ,KN⊥AB于N,
∵OC=OA,
∴PL=PA ,
∵PA=CQ,
∴PL=CQ,
∴△PGL≌△QGC,
∴GP=GQ,
∵OG=![]() ,
,
∴PQ=![]() ,
,
在Rt△OPQ中,得(4-t)2+(4+t)2=![]() ,
,
∴t=2 ,
∵△PDG为等腰直角三角形,
∴四边形PGDK为正方形,
∵OQ=6,
∴GM=3,
∵GP=GO,
∴PM=MO=1,
∵△GMP≌△PNK,
∴GM=PN=3,PM=KN=1,
∴AN=5,ON=1,
∴K(1,-1)


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使PC是⊙O的切线.
(1)求证:∠PCA=∠ABC;
(2)若∠P=60°,PC=4,求PE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
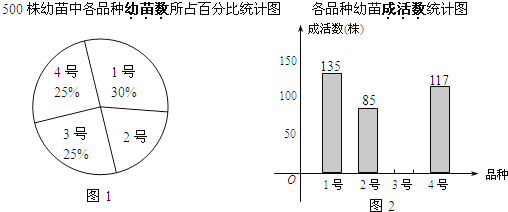
(1)实验所用的2号茶树幼苗的数量是 株;
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
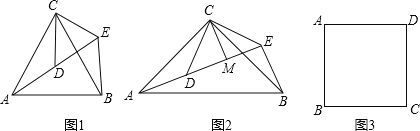
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为 ;
②线段AD,BE之间的数量关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,CD=3,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
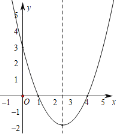
(1)求该抛物线的解析式;
(2)如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A(2,1),B两点.
的图象相交于A(2,1),B两点.
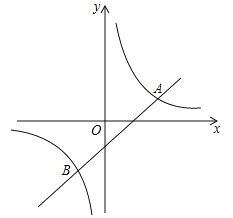
(1)求出反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出使反比例函数值大于一次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“淮南牛肉汤”是安徽知名地方小吃.某分店经理发现,当每碗牛肉汤的售价为6元时,每天能卖出500碗;当每碗牛肉汤的售价每增加0.5元时,每天就会少卖出20碗,设每碗牛肉汤的售价增加![]() 元时,一天的营业额为
元时,一天的营业额为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出
的函数关系式(不要求写出![]() 的取值范围);
的取值范围);
(2)考虑到顾客可接受价格![]() 元/碗的范围是
元/碗的范围是![]() ,且
,且![]() 为整数,不考虑其他因素,则该分店的牛肉汤每碗多少元时,每天的牛肉汤营业额最大?最大营业额是多少元?
为整数,不考虑其他因素,则该分店的牛肉汤每碗多少元时,每天的牛肉汤营业额最大?最大营业额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某竹制品加工厂根据市场调研结果,对该厂生产的一种新型竹制品玩具未来两年的销售进行预测,并建立如下模型:设第t个月,竹制品销售量为P(单位:箱),P与t之间存在如图所示函数关系,其图象是线段AB(不含点A)和线段BC的组合.设第t个月销售每箱的毛利润为Q(百元),且Q与t满足如下关系Q=2t+8(0≤t≤24).
(1)求P与t的函数关系式(6≤t≤24).
(2)该厂在第几个月能够获得最大毛利润?最大毛利润是多少?
(3)经调查发现,当月毛利润不低于40000且不高于43200元时,该月产品原材料供给和市场售最和谐,此时称这个月为“和谐月”,那么,在未来两年中第几个月为和谐月?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,测第70次旋转结束时,点D的坐标为_____.
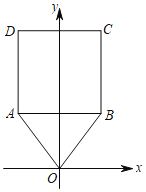
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com