
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
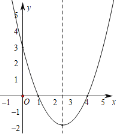
(1)求该抛物线的解析式;
(2)如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.
【答案】(1)![]() ;(2)存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;(3)Q的坐标
;(2)存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;(3)Q的坐标![]() 或
或![]() .
.
【解析】
(1)将A(1,0)、B(4,0)、C(0,3)代入y=ax2+bx+c,求出a、b、c即可;
(2)四边形PAOC的周长最小值为:OC+OA+BC=1+3+5=9;
(3)分两种情况讨论:①当△BPQ∽△BCA,②当△BQP∽△BCA.
解:(1)由已知得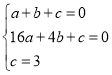 ,
,
解得 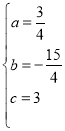
所以,抛物线的解析式为![]() ;
;
(2)∵A、B关于对称轴对称,如下图,连接BC,与对称轴的交点即为所求的点P,此时PA+PC=BC,
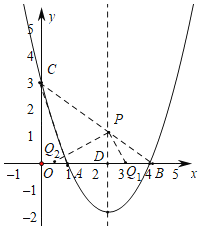
∴四边形PAOC的周长最小值为:OC+OA+BC,
∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC=5,
∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;
(3)如上图,设对称轴与x轴交于点D.
∵A(1,0)、B(4,0)、C(0,3),
∴OB=4,AB=3,BC=5,
直线BC:![]() ,
,
由二次函数可得,对称轴直线![]() ,
,
∴![]() ,
,
①当△BPQ∽△BCA,
![]() ,
,
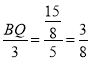 ,
,
![]() ,
,
![]() ,
,
![]()
②当△BQP∽△BCA,
![]() ,
,
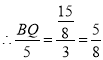 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上,求得点Q的坐标![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
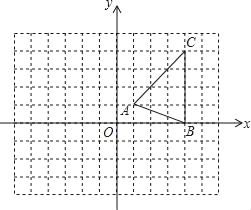
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.
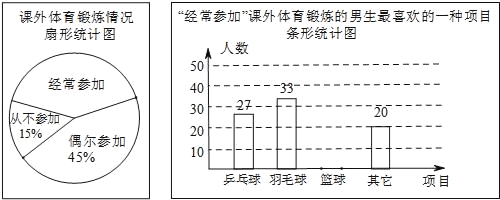
请根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为________;
(2)请补全条形统计图;
(3)该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
(4)小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1200×![]() =108”,请你判断这种说法是否正确,并说明理由.
=108”,请你判断这种说法是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.
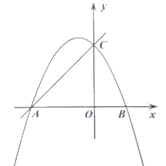
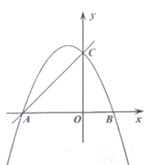
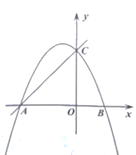
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为第一象限内的一点,当
为第一象限内的一点,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,连接
为斜边的等腰直角三角形时,连接![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并写出自变量
,并写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,连接![]() 、
、![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置(
的位置(![]() 与
与![]() 对应),若
对应),若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:一般地,![]() 个相同的因数
个相同的因数![]() 相乘
相乘 ![]() ,记为
,记为![]() .如
.如![]() ,此时,
,此时,![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).一般地,若
).一般地,若![]() ,(
,(![]() 且
且![]() ,
,![]() ),则
),则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).如
).如![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记为
的对数,记为![]() (即
(即![]() ).
).
(1)计算以下各对数的值:![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(2)观察(1)中三数![]() 、
、![]() ,
,![]() 之间满足怎样的关系式,
之间满足怎样的关系式,![]() 、
、![]() 、
、![]() 之间又满足怎样的关系式;
之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?![]() __________.(
__________.(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根据幂的运算法则:![]() 以及对数的含义证明上述结论.
以及对数的含义证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a﹣2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com