练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某校在开展读书交流活动中全体师生积极捐书．为了解所捐书籍的种类，对部分书籍进行了抽样调查，李老师根据调查数据绘制了如图所示不完整统计图．请根据统计图回答下面问题：
    （1）本次抽样调查的书籍有多少本？请补全条形统计图；
    （2）求出图1中表示文学类书籍的扇形圆心角度数；
    （3）本次活动师生共捐书1200本，请估计有多少本科普类书籍？

    【答案】
    （1）解；8÷20%=40（本），

    其它类；40×15%=6（本），

    补全条形统计图，如图2所示


    （2）解；文学类书籍的扇形圆心角度数为：360× =126°
    （3）解；普类书籍有： ×1200=360（本）
    【解析】（1）根据已知条件列式计算即可，如图2所示，先计算出其它类的频数，再画条形统计图即可；（2）根据已知条件列式计算即可；（3）根据已知条件列式计算即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2﹣2x+3与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1 ， 将C1关于点B的中心对称得C2 ， C2与x轴交于另一点C，将C2关于点C的中心对称得C3 ， 连接C1与C3的顶点，则图中阴影部分的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），扇形AOB中，OA=10，∠AOB=36°．若固定B点，将此扇形依顺时针方向旋转，得一新扇形A′O′B，其中O′点在直线BA上，如图（2）所示，则O点旋转至O′点所经过的轨迹长度（弧长）为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究证明：
    （1）如图1，在△ABC中，AB=AC，点E是BC上的一个动点，EG⊥AB，EF⊥AC，CD⊥AB，点G，F，D分别是垂足．求证：CD=EG+EF；
    猜想探究：

    （2）如图2，在△ABC中，AB=AC，点E是BC的延长线上的一个动点，EG⊥AB于G，EF⊥AC交AC延长线于F，CD⊥AB于D，直接猜想CD、EG、EF之间的关系为；

    （3）如图3，边长为10的正方形ABCD的对角线相交于点O、H在BD上，且BH=BC，连接CH，点E是CH上一点，EF⊥BD于点F，EG⊥BC于点G，则EF+EG= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．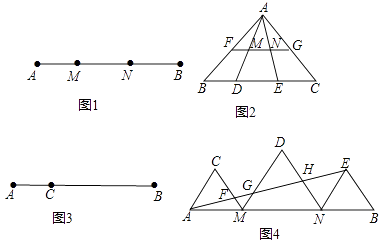

    （1）已知点M，N是线段AB的勾股分割点，若AM=2，MN=3，求BN的长；
    （2）如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC＞DE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点；
    （3）已知点C是线段AB上的一定点，其位置如图3所示，请在BC上画一点D，使点C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画一种情形即可）；
    （4）如图4，已知点M，N是线段AB的勾股分割点，MN＞AM≥BN，△AMC，△MND和△NBE均为等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究S△AMF ， S△BEN和S四边形MNHG的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的弦BC长为8，点A是⊙O上一动点，且∠BAC=45°，点D，E分别是BC，AB的中点，则DE长的最大值是（ ）

    A.4
    B.4
    C.8
    D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2015年6月28日，“合福高铁”正式开通，对南平市的旅游产业带来了新的发展机遇．某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数，并将调查结果绘制成如下两幅不完整的统计图表，请根据图表信息回答下列问题：

    景点

    频数
    （人数）

    频率

    九曲溪

    116

    0.29

    归宗岩

    0.25

    天成奇峡

    84

    0.21

    溪源峡谷

    64

    0.16

    华阳山

    36

    0.09


    （1）此次共调查人，
    （2）补全条形统计图；
    （3）由上表提供的数据可以制成扇形统计图，则“天成奇峡”所对扇形的圆心角为°；
    （4）该旅行社预计今年8月份将要接待来以上景点的游客约2 500人，根据以上信息，请你估计去“九曲溪”的游客大约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在矩形ABCD中， =a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．

    （1）如图1，当DH=DA时，填空：∠HGA=度；
    （2）如图1，当DH=DA时，若EF∥HG，求∠AHE的度数，并求此时的最小值；
    （3）如图3，∠AEH=60°，EG=2BG，连接FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx+3（a≠0）过A（4，4），B （2，m）两点，点B到抛物线对称轴的距离记为d，满足0＜d≤1，则实数m的取值范围是 ．

    查看答案和解析>>

    同步练习册答案