
【题目】有一组邻边相等,并且有一个角是直角的平行四边形是正方形,因此正方形是四边相等,四角相等的四边形.
初二数学兴趣小组开展了一次课外活动,过程如下:如图,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.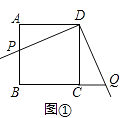
(1)求证:DP=DQ
(2)如图②,小聪在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;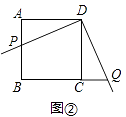
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小聪算出△DEP的面积.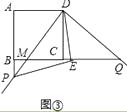
【答案】
(1)
证明:∵∠ADC=∠PDQ=90°,
∴∠ADP=∠CDQ.
在△ADP与△CDQ中, 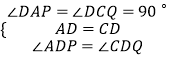
∴△ADP≌△CDQ(ASA),
∴DP=DQ
(2)
证明:猜测:PE=QE.
证明:由(1)可知,DP=DQ.
在△DEP与△DEQ中, 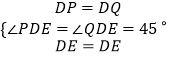
∴△DEP≌△DEQ(SAS),
∴PE=QE
(3)
解:∵AB:AP=3:4,AB=6,
∴AP=8,BP=2.
与(1)同理,可以证明△ADP≌△CDQ,
∴CQ=AP=8.
与(2)同理,可以证明△DEP≌△DEQ,
∴PE=QE.
设QE=PE=x,则BE=BC+CQ﹣QE=14﹣x.
在Rt△BPE中,由勾股定理得:BP2+BE2=PE2,
即:22+(14﹣x)2=x2,
解得:x= ![]() ,即QE=
,即QE= ![]() .
.
∴S△DEQ= ![]() QECD=
QECD= ![]() ×
× ![]() ×6=
×6= ![]() .
.
∵△DEP≌△DEQ,
∴S△DEP=S△DEQ= ![]()
【解析】(1)证明△ADP≌△CDQ,即可得到结论:DP=DQ;(2)证明△DEP≌△DEQ,即可得到结论:PE=QE;(3)与(1)(2)同理,可以分别证明△ADP≌△CDQ、△DEP≌△DEQ.在Rt△BPE中,利用勾股定理求出PE(或QE)的长度,从而可求得S△DEQ= ![]() ,而△DEP≌△DEQ,所以S△DEP=S△DEQ
,而△DEP≌△DEQ,所以S△DEP=S△DEQ ![]() .
.
【考点精析】掌握全等三角形的性质是解答本题的根本,需要知道全等三角形的对应边相等; 全等三角形的对应角相等.


科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 平行四边形是中心对称图形
B. 斜边及一锐角分别相等的两直角三角形全等
C. 两个锐角分别相等的两直角三角形全等
D. 一直角边及斜边分别相等的两直角三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.
斐波那契数列中的第n个数可以用![]() [(
[(![]() )n﹣(
)n﹣(![]() )n]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
)n]表示(其中,n≥1).这是用无理数表示有理数的一个范例.
任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏扬州的旅游宣传口号是“诗画瘦西湖,人文古扬州.给你宁静,还你活力”.为了了解广大市民对这一旅游宣传口号的知晓率,应采用的合适的调查方式为_____.(填“普查”或“抽样调查”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了更好得节约能源,决定购买一批节省能源的10台新机器。现有甲、乙两种型号的设备,其中每台的价格、工作量如下表。经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台甲型设备比购买3台乙型设备少6万元.
甲型 | 乙型 | |
价格(万元/台) |
|
|
产量(吨/月) | 240 | 180 |
(1)求a, b的值;
(2)经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;
(3)在(2)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
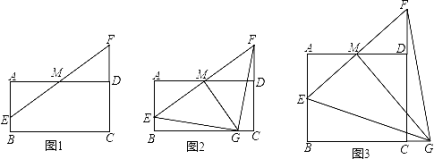
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形
(3)如图3,若AB=![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com