
已知,如图,在Rt△ABC中,∠C=90º,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;(2分+4分)
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=6,BD=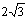 ,
,
求⊙O的半径.(4分)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
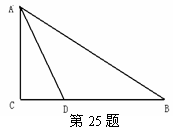
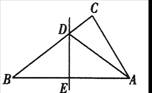
如图4,△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,
△ADC的周长为9cm,则△ABC的周长是( )
A.10cm B.12cm C.17cm D.15cm
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
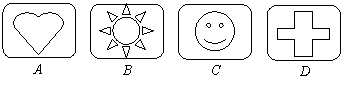
有四张 背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图),小刚同学将这四张
背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图),小刚同学将这四张 卡片背面朝上洗匀
卡片背面朝上洗匀 摸出一张,放回洗匀再摸出一张.(1)用树状图(或列表法)表示两次摸出卡片所有可能的结果;(卡片用A、B、C、D表示)(2)求摸出的
摸出一张,放回洗匀再摸出一张.(1)用树状图(或列表法)表示两次摸出卡片所有可能的结果;(卡片用A、B、C、D表示)(2)求摸出的 两张卡片图形都是中心对称图形的概率. (4分+4分)
两张卡片图形都是中心对称图形的概率. (4分+4分)
 |
、
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=3,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
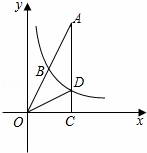
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=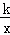 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com