
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 分别根据三角形内角和定理、勾股定理的逆定理对各选项进行逐一分析即可.
解答 解:①∵a2+b2=$\frac{289}{4}$=($\frac{17}{2}$)2,c2=(8$\frac{1}{2}$)2=($\frac{17}{2}$)2
∴a2+b2=c2,
∴此三角形是直角三角形,故本小题正确;
②∵a2:b2:c2=1:3:2,
∴设a2=x,则b2=3x,c2=2x,
∵x+2x=3x,
∴a2+c2=b2,
∴此三角形是直角三角形,故本小题正确;
③∵∠A:∠B:∠C=3:4:5,
∴设∠A=3x,则∠B=4x,∠C=5x.
∵∠A+∠B+∠C=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=45°,∠B=60°,∠C=75°,
∴此三角形不是直角三角形,故本小题错误;
④∵∠A=2∠B=2∠C,
∴设∠B=∠C=x,则∠A=2x,
∴x+x+2x=180°,
解得:x=45°,
∴∠A=2x=90°,
∴此三角形是直角三角形,故本小题正确.
故选C.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
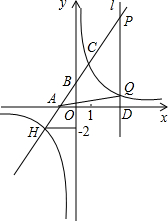 在平面直角坐标系xOy中,直线y=2x+2与x轴、y轴分别交于点A、B,与双曲线$y=\frac{k}{x}$交于第一象限的点C(1,m)和第三象限的点H,H点的纵坐标为-2
在平面直角坐标系xOy中,直线y=2x+2与x轴、y轴分别交于点A、B,与双曲线$y=\frac{k}{x}$交于第一象限的点C(1,m)和第三象限的点H,H点的纵坐标为-2查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{a}$(a≥0) | C. | $\sqrt{{a^2}+1}$ | D. | $\sqrt{-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
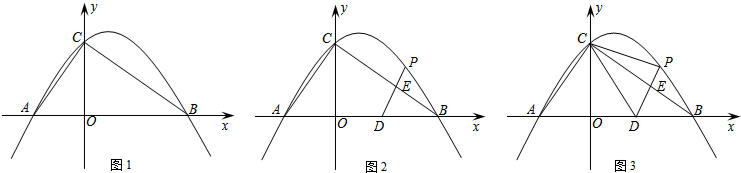
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com