
分析 (1)直接找出最简公分母进而化简求出即可;
(2)利用已知进而分别化简二次根式求出即可.
解答 解:(1)$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\sqrt{5}$-$\sqrt{3}$;
(2)$\frac{2}{\sqrt{3}+1}$+$\frac{2}{\sqrt{5}+\sqrt{3}}$+$\frac{2}{\sqrt{7}+\sqrt{5}}$+…+$\frac{2}{\sqrt{2015}+\sqrt{2013}}$
=$\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+…+$\sqrt{2015}$-$\sqrt{2013}$
=$\sqrt{2015}$-1.
点评 此题主要考查了分母有理化,正确找出有理化因式是解题关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x-2}$ | B. | $\sqrt{2-x}$ | C. | $\sqrt{{x}^{2}-2}$ | D. | $\sqrt{2-{x}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
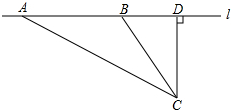 校车安全是近几年社会关注的重大问题.某数学活动小组设计了如下检测校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD=30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时3秒,这辆校车是否超速?说明理由.
校车安全是近几年社会关注的重大问题.某数学活动小组设计了如下检测校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD=30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时3秒,这辆校车是否超速?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com