
分析 根据题意画出相应的图形,如图所示,分四种情况考虑:当AC垂直于x轴;当BC垂直于x轴;当C在第二象限,且AC⊥BC;当C在第四象限,且AC⊥BC,分别求出C的坐标即可.
解答 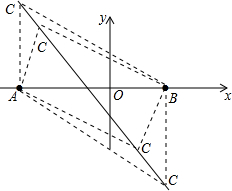 解:画出相应的图形,如图所示,分四种情况考虑:
解:画出相应的图形,如图所示,分四种情况考虑:
设C坐标为(a,-$\sqrt{3}$(a+1)),
当AC⊥x轴时,C坐标为(-4,3$\sqrt{3}$);
当BC⊥x轴时,C坐标为(2,-3$\sqrt{3}$);
当AC⊥BC时,kAC•kBC=-1,即$\frac{-\sqrt{3}(a+1)}{a+4}$•$\frac{-\sqrt{3}(a+1)}{a-2}$=-1,
整理得:4a2+8a-5=0,即(2a-1)(2a+5)=0,
解得:a=$\frac{1}{2}$或a=-$\frac{5}{2}$,
当a=$\frac{1}{2}$时,C坐标为($\frac{1}{2}$,-$\frac{3\sqrt{3}}{2}$);
当a=-$\frac{5}{2}$时,C坐标为(-$\frac{5}{2}$,$\frac{3\sqrt{3}}{2}$),
综上,点C的坐标为(-4,3$\sqrt{3}$),(2,-3$\sqrt{3}$),(-$\frac{5}{2}$,$\frac{3\sqrt{3}}{2}$),($\frac{1}{2}$,-$\frac{3\sqrt{3}}{2}$).
故答案为:(-4,3$\sqrt{3}$),(2,-3$\sqrt{3}$),(-$\frac{5}{2}$,$\frac{3\sqrt{3}}{2}$),($\frac{1}{2}$,-$\frac{3\sqrt{3}}{2}$)
点评 此题属于一次函数综合题,涉及的知识有:两直线垂直时斜率满足的关系,一元二次方程的解法-因式分解法,利用了数形结合及分类讨论的思想,分类讨论时考虑问题要全面,做到不重不漏.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
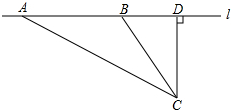 校车安全是近几年社会关注的重大问题.某数学活动小组设计了如下检测校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD=30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时3秒,这辆校车是否超速?说明理由.
校车安全是近几年社会关注的重大问题.某数学活动小组设计了如下检测校车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD=30米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时3秒,这辆校车是否超速?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
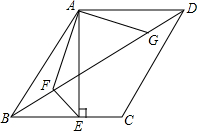 如图,在?ABCD中,AE⊥BC于点E,AE=AD,点F、G是对角线BD上的两点,且△AFG是等腰三角形,∠FAG=90°,若AF=3$\sqrt{2}$,EF=2,则?ABCD的面积为34.
如图,在?ABCD中,AE⊥BC于点E,AE=AD,点F、G是对角线BD上的两点,且△AFG是等腰三角形,∠FAG=90°,若AF=3$\sqrt{2}$,EF=2,则?ABCD的面积为34.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
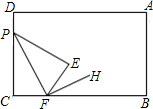 如图,将长方形纸片ABCD的角C沿PF折叠,使点C落在长方形的内部点E处,若FH平分∠BFE,则∠PFH的度数( )
如图,将长方形纸片ABCD的角C沿PF折叠,使点C落在长方形的内部点E处,若FH平分∠BFE,则∠PFH的度数( )| A. | 90°<a<180° | B. | 0°<a<90° | ||
| C. | a=90° | D. | a随折痕FH位置的变化而变化 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
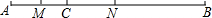 如图,线段AB=9cm,BC=6cm,点M是AC的中点.
如图,线段AB=9cm,BC=6cm,点M是AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
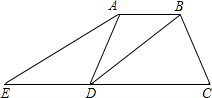 如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com